Учет и устранение неопределенностей в процессе проектирование систем
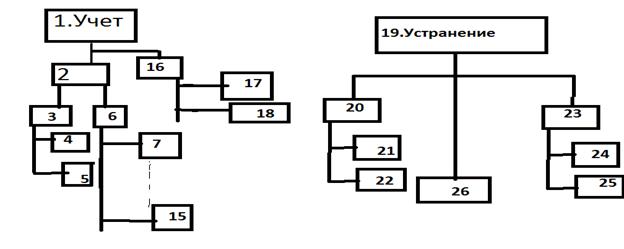
1.Неопределенный фактор(НФ)-опред. среда, ситуация на рынке, требование заказчика
2.методика приема 3.приформ. исх. данных 4.равнозначный анализ 5.огранич. числа стратегий 6. при разраб.матем. моделей 7.выделение уравнений моделей 8.приемы доминирования.9.выделение этапов операций 10.районирование множества векторов 11. Построение функцион. Критериев. 12.анализ чувствительности 13.усилительный анализ 14.уравнительный анализ 15.построение обобщенных показателей 16 ---
17- по условию применения 18. По системе 20. разработка вариантов 21. паралл. разработка вариантов 22.паралл. при большой стоимости 23 уточнение исходных данных 24-прогноз 25-методы экспертных оценок 26 реализация компенсационных возможностей
16.1 – Методика структ. Анализа с использованием ф-ции полезности
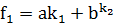 - пример ф-ции полезности
- пример ф-ции полезности
1. Мн-во конкурир. Структур;Мн-во частн. показат.;Мн-во условий функционир.; Матрица ограничений показат.; Ф-ции полезн. для частн. показат.; М-ца бинарных предпочтений;Модели для оценки частых показателей; Матрица числов. векторн.;Оценка полезн. конкурир. Структур; Оценка структур в диапазоне условий.
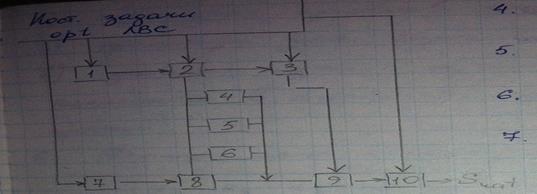
ПРИМЕР. Множество конкурирующих структур {Si}:S1,S2,S3.
Множество частных критериев {Kj}. Пусть будет 4 частных критерия: K1, K2, K3, K4; K1 — время реакции системы;K2 — коэффициент загрузки процессора;K3 — пропускная способность системы;K4 — стоимость процессорных устройств
1. Множество вариантов условий:
M = 1, т.е. N = 14 — пессимистическая оценка с весом 1;M = 2, т.е. N = 17 — наиболее вероятная оценка с весом 4;M = 3, т.е. N = 20 — оптимистическая оценка с весом 1;т.е. вероятность этого возникновения варианта условий (1);P1 = 0,17;P2 = 0,66;P3 = 0,17;
2. Матрица критериальных ограничений
3. Должны построить функции полезности
Функции полезности частных критериев, которые используются при приведении векторных оценок к безразмерному виду. При этом худшее значение критерия соответствует полезности 0. Лучшее значение — полезности 1, а промежуточные значения подвергаются линейной апроксимации. Предполагается, что полезность сверх худших значениях критерия много меньше нуля. Полезность сверх лучших значений = 1.
4. Матрица бинарных предпочтений и соответствующие веса частных критериев
5. Т.е. (∑ по строке)/(∑Cj)
6. Cj = 1,5 + 0,5 + 1 + 3 = 2
7. K1 д.б. > K3 (иначе не выполняется условие тр-ти).
8. В реальной экспертизе получилась такая матрица. В ней есть ошибки эксперта, так как эксперт, который оаботает, может быть не последовательным. Есть правило проверки на транзированность. Если оно нарушается, следовательно эксперт допустил ошибку (а>b, b>c, следовательно a>c) (> — лучше).
9. Модели для оценки частных критериев. Для критериев K1, K2, K3 используется аналитическая модель локальной ИВС. Для критерия K4 необходимые оценки определяются расчетным путем.
10. Матрица векторных оценок для M = 1 и соответствующие веса частных критериев (т.е. к системе подключаются 14 терминов).
11. Матрица векторных оценок для M = 2 и соответствующие веса частных критериев
12. Матрица векторных оценок для M = 3 и соответствующие веса частных критериев
13. Вес расчитывается в результате нормировки по всем критериям
14. Оценка полезности конкурирующих структур для M = 1
15. Оценка полезности конкурирующих структур для M = 2
16. Оценка полезности конкурирующих структур для M = 3
17. Оценка полезности конкурирующих структур в диапазоне условий
Вывод: в заданных условиях рациональной является структура S2.
