Временные диаграммы модулирующего b(t) и модулированного U(t) сигналов, соответствующие передаче 9-го уровня сообщения a(t)

Содержание

Содержание. 1

Задание на курсовую работу: 2

1. Источник сообщений. 3

2. Дискретизатор. 6

3. Кодер. 9

4. Модулятор. 11

5. Канал связи. 16

6. Демодулятор. 18

7. Декодер. 21

8. Фильтр – восстановитель. 23

Источник сообщений.

Источник сообщений выдает сообщение a(t), представляющее собой непрерывный стационарный случайный процесс, мгновенные значения которого в интервале [a_min; a_max] распределены по заданному закону, а мощность сосредоточена в полосе частот от 0 до F_c.

1.1.

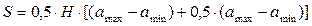-площадь равнобедренной трапеции.

Одномерная плотность вероятности мгновенных значений сообщения a(t) описывается системой вида:

P(a)=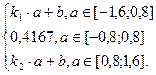

1.2. Найдем математическое ожидание:

.

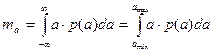Найдем дисперсию:

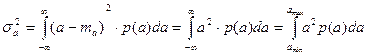
Найдем СКО:

.

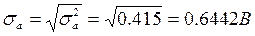2. Дискретизатор.

Передача непрерывного процесса осуществляется дискретными методами. Для этого сообщение а(t) дискретизируется по времени и квантуется по уровню с равномерным шагом. Шаг квантования по уровню Dа= 0,1В.

2.1. . Найдем шаг дискретизации по времени. Для этого воспользуемся теоремой Котельникова 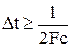, тогда iаг дискретизации по времени:

2.2. Число уровней квантования L при равномерном шаге определяется как частное от деления размаха сигнала на шаг квантования Dа. Т.к. шаг квантования по уровню Dа задан, то число уровней квантования:

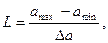
2.3. Шум квантования представляет собой стационарный случайный процесс с независимыми значениями отдельных отсчетов e = aд – a (эпсилон). Если в качестве квантованного значения a принимается ближайший дискретный уровень, то шум квантования e (ошибка дискретизатора, возникающая из-за того, что не происходит переход на другой уровень) при равномерном квантовании с шагом Da находится в пределах

,

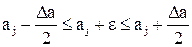
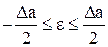здесь e –шум квантования.

Поскольку квантование по уровню ведется с равномерным шагом,то закон распределения плотности вероятности шума квантования ω_ш(ε) также будет равномерным и не будет зависеть от номера интервала квантования:

Найдем среднюю мощность (дисперсия шума квантования):

2.4. Энтропия – средняя информативность источника на один символ, определяющая неожиданность выдаваемых сообщений для источника без памяти энтропия определяется по формуле:

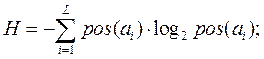
Определим вероятность на интервале

Определим производительность источника, как энтропию в единицу времени:

.

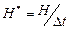Кодер.

Кодирование осуществляется в два этапа.

Первый этап: производится примитивное кодирование каждого уровня квантованного сообщения k- разрядным двоичным кодом.

Второй этап: к полученной k-разрядной двоичной кодовой комбинации добавляются проверочные символы, формируемые в соответствии с правилами кодирования по коду Хэмминга.

В результате этих преобразований на выходе кодера образуется синхронная двоичная случайная последовательность b(t) (синхронный случайный телеграфный сигнал), состоящая из последовательности биполярных импульсов единичной высоты, причем положительные импульсы в ней соответствуют символу «0», а отрицательные – символу «1» кодовой комбинации.

Для кодирования Lуровней квантованного сообщения число разрядов двоичной кодовой комбинации:

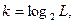
k .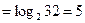

3.2. Вычислим избыточность кода при использовании кодирования Хэмминга:

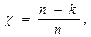
Модулятор.

В модуляторе синхронная двоичная случайная последовательность биполярных импульсов b(t) осуществляет модуляцию гармонического переносчика e(t)=U_m cos(2πft), U_m=1В, f = 100 V’_n)

Для частотной модуляции (ЧМ):

«0» − U₀(t) = U_m cos(2π(f- 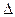f)t);

«1» − U₁(t) = U_m cos(2π(f+ 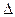f)t).

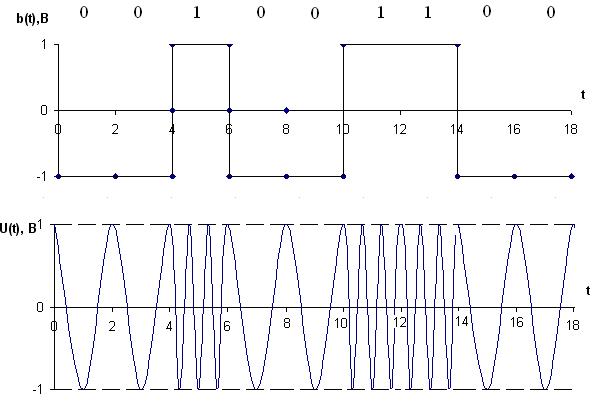
Временные диаграммы модулирующего b(t) и модулированного U(t) сигналов, соответствующие передаче 9-го уровня сообщения a(t).

4.3. Корреляционная функция модулирующего сигнала k(τ):

,

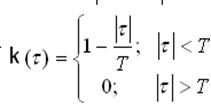График корреляционной функции модулирующего сигнала k(τ)

4.4. Cпектральная плотность мощности модулирующего сигнала G_В(ω).

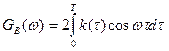
Ширина энергетического спектра модулирующего сигнала: 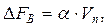где α=1.

4.6. Энергетический спектр G_u(ω) ЧМ сигнала представляет собой сумму энергетических спектров АМ сигналов с несущими частотами f₁= f₀ –∆f и

f₂= f₀ –∆f.

G_u(f) = 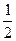G_B(f–f₁)+ 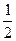G_B(f–f₂),

G_u(f) = 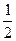G_B(f–2,43∙10⁷)+ 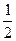G_B(f–2,727∙10⁷).

Энергетический спектр G_u(ω) ЧМ сигнала

4.7. Ширина энергетического спектра ∆F_u модулированного сигнала:

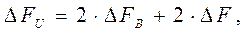
Канал связи

Передача сигнала U(t) осуществляется по каналу с постоянными параметрами и аддитивным флуктуационным шумом n(t) с равномерным энергетическим спектром N₀/2 (белый шум).

Сигнал на выходе такого канала можно записать следующем образом:

z(t) = U(t) + n(t).

5.1. Мощность шума в полосе частот F_k = ,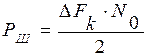

5.2. Найдем отношение сигнал-шум:

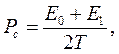
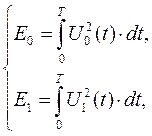
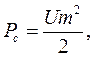
Тогда .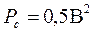

Отношение сигнал – шум Р_с /Р_ш:

5.3. Пропускная способность канала:

С = ∆F_U·log₂(1+P_c/P_Ш),

5.4. Эффективность использования пропускной способности канала Кс определяется как отношение производительности источника Н^’к пропускной способности канала С.

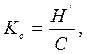
Демодулятор

В демодуляторе осуществляется оптимальная когерентная или некогерентная (в зависимости от варианта) обработка принимаемого сигнала z(t) = U(t) + n(t).

Алгоритм оптимального приема по критерию минимума средней вероятности ошибки при равновероятных символах в детерминированном канале с белым гауссовским шумом:

при выполнении неравенства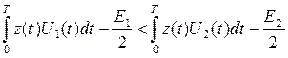

регистрируется символ «1»;

Если 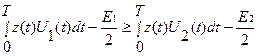, то регистрируется символ «0».

Декодер

В декодере декодирование осуществляется в два этапа. На первом этапе производится обнаружение и исправление ошибки в кодовой комбинации. Считать, что ошибка произошла в i-ом разряде. На втором этапе из нее выделяются информационные символы, а затем k – разрядная двоичная кодовая комбинация преобразуется в элемент квантованного сообщения.

Наименьшее расстояние по Хеммингу между кодовыми комбинациями:

;

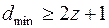7.3. Вероятность необнаружения ошибки:

,

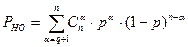где n – число разрядов кодовой последовательности, n = 9;

q – обнаруживающая способность кода Хэмминга;

р – вероятность ошибки в одном разряде, p = 0,006.

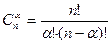– общее число различных выборок (сочетаний) объема a.