Однородное дифференциальное уравнение первого порядка (31)
Функция f(x,y) называется однородной функцией относительно переменной x,y n-го порядка если для любого λ, f(λx, λy)= λnf(x,y). Дифференциальное уравнение 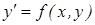 называется однородным дифференциальным уравнением если
называется однородным дифференциальным уравнением если 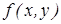 однородная функция нулевого порядка, т. е.
однородная функция нулевого порядка, т. е. 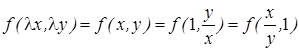 . Для нахождения решения однородного дифференциального уравнения делают подстановку
. Для нахождения решения однородного дифференциального уравнения делают подстановку 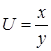 или
или 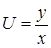 отсюда находят
отсюда находят 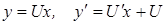 и подставляют в дифференциальное уравнение получим:
и подставляют в дифференциальное уравнение получим: 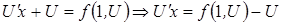 - дифференциальное уравнение с разделяющими переменными. Получаем
- дифференциальное уравнение с разделяющими переменными. Получаем 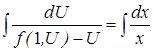 проинтегрируем пологая что
проинтегрируем пологая что 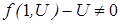 и исследуем отдельно. Примечание: дифференциальное уравнение
и исследуем отдельно. Примечание: дифференциальное уравнение 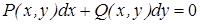 является однородным дифференциальным уравнением, если P(x,y) и Q(x,y) однородные функции одного и того же порядка.
является однородным дифференциальным уравнением, если P(x,y) и Q(x,y) однородные функции одного и того же порядка.
3. Дифференциального уравнения первого порядка приводящейся к однородным:
Дифференциальное уравнения первого порядка вида 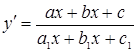 приводятся либо к однородным дифференциальным уравнениям, либо к дифференциальным уравнениям с разделяющими переменными. а. При с=с1=0 это очевидно:
приводятся либо к однородным дифференциальным уравнениям, либо к дифференциальным уравнениям с разделяющими переменными. а. При с=с1=0 это очевидно: 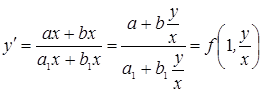 . б.Пусть
. б.Пусть 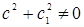 тогда делают подстановку:
тогда делают подстановку: 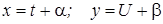 , где
, где 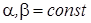 ,
, 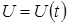 , t – новая переменная
, t – новая переменная 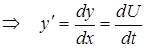 , тогда
, тогда 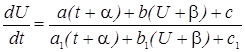 или
или 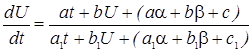 , потребуем чтобы
, потребуем чтобы 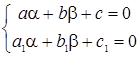 эта система линейных уравнений относительно
эта система линейных уравнений относительно 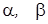 неоднородна, она имеет единственное решение если ее определитель
неоднородна, она имеет единственное решение если ее определитель 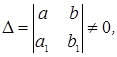 т.е.
т.е. 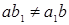 тогда
тогда 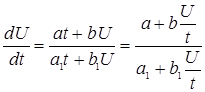 - однородное дифференциальные уравнения относительно функции U находим его общий интеграл
- однородное дифференциальные уравнения относительно функции U находим его общий интеграл 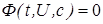 , а следовательно находим и решение исходного дифференциального уравнения
, а следовательно находим и решение исходного дифференциального уравнения 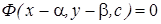 . с.Пусть
. с.Пусть 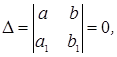 т. е.
т. е. 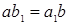 или
или 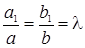 отсюда
отсюда  и следовательно мы можем записать
и следовательно мы можем записать 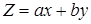 или
или 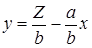
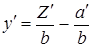 тогда
тогда 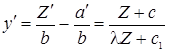
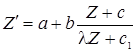 - дифференциальное уравнение с разделяющимися уравнениями.
- дифференциальное уравнение с разделяющимися уравнениями.
Замечание: д.у. вида 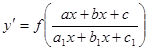 , где
, где 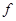 -непрерывная функция, интегрируется также , как и д.у., рассматриваемое в этом пункте.
-непрерывная функция, интегрируется также , как и д.у., рассматриваемое в этом пункте.
Линейное дифференциальное уравнение первого порядка. Уравнение Бернулли (32).
Д.у. вида 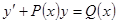 , где
, где 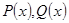 -постоянные или непрерывные функции ~x называются линейными д.у. первого порядка. Неоднородным, если
-постоянные или непрерывные функции ~x называются линейными д.у. первого порядка. Неоднородным, если 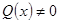 и однородным, если
и однородным, если 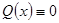 . Его решение ищут в виде
. Его решение ищут в виде 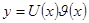
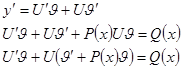
Так как у нас имеется лишняя степень свободы, то на одну из функции наложим дополнительное условие, в нашем случае потребуем, чтобы 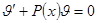 , тогда для функции
, тогда для функции 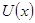 получим уравнение
получим уравнение 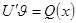
Итак, 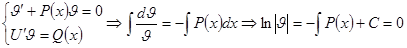
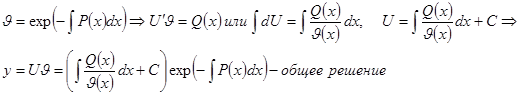
Замечание:линейное д.у. первого порядка, когда 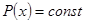 , т.е. д.у. вида
, т.е. д.у. вида 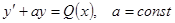 может быть решено и другим способом, как линейное д.у. первого порядка с постоянными коэффициентами.
может быть решено и другим способом, как линейное д.у. первого порядка с постоянными коэффициентами.
К линейным д.у. первого порядка примыкает и уравнение Бернулли, т.е. уравнение вида: 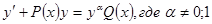 Это уравнение можно привести к линейному д.у. подстановкой
Это уравнение можно привести к линейному д.у. подстановкой 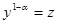
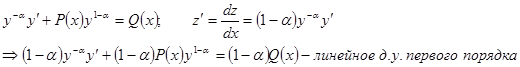
Замечание:
1) К уравнению Бернулли приводит задача о движении тела в среде, когда сила сопротивления среды зависит от скорости нелинейно, т.е. 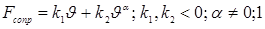
2) Решая уравнение Бернулли ищут , не приводя его к линейному подстановкой 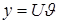 , т.е. как линейное.
, т.е. как линейное.
