Существование эйлерова цикла и эйлерова пути

Оптимизационные задачи на графах

Основные понятия теории графов

Граф G – это совокупность множества вершин V и множества ребер X: G=<V, X>, где V – непустое множество. Множество X состоит из пар элементов мнoжества V.

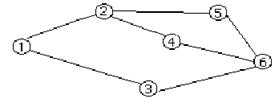
Рис. 8.1. Граф G=<V, X>.

На данном графе (рис. 8.1) шесть вершин, т.е. V: 1, 2, 3, 4, 5, 6 и семь ребер, т.е. Х: <1, 2>, <1, 3>, <2, 5>, <2, 4>, <3, 6>, <4, 6>, <5, 6>.

Если пары в наборе Х повторяются, то граф называется псевдографом или графом с кратными ребрами.

Ребро, начало и конец которого совпадают, называется петлей.

Вершины называются смежными или соседними, если существует ребро, их соединяющее. То есть вершины v₁ и v₂ смежные, так как <v₁, v₂> 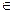X, где X – множество ребер рассматриваемого графа G=<V, X>.

Если вершина является началом или концом ребра, то вершина и ребро называются инцидентными.

Степенью вершины v называется число инцедентных ей ребер. Обозначается d(v).

Вершина, степень которой равна нулю, называется изолированной.

Вершина, степень которой равна единице, называется висячей или тупиковой.

Маршрутом в графе называется последовательность вершин и ребер, в которой конец предыдущего ребра совпадает с началом следующего (это не относится к первому и последнему ребру). Число ребер в маршруте определяет его длину.

Если элементы в парах множества Х не упорядочены, то граф G называют неориентированным.

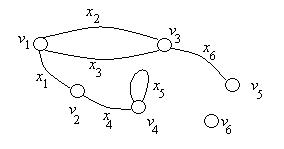
Рис. 8.2. Граф с кратными ребрами.

На графе, изображенном на рисунке 8.2 верщина v₅ является висячей, так как d(v₅)=1. Степень вершины v₆ равна нулю d(v₆)=0, эта вершина v₆ изолированная.Ребро х₅= <v₄, v₄>является петлей. Ребра х₂ = <v₁, v₂> и х₃ = <v₁, v₂> смежные или соседние. Пример маршрута в графе рисунка …. (v ₁, v₃, v₅). Маршрут содержит два ребра, значит, его длина равна 2. Также этот маршрут можно описать с помощью ребер, что позволяет уточнить маршрут: (v₁, х₂, v₃, х₆, v₅).

Плоский граф

Граф, ребра которого не пересекаются, называется плоским (планарным) графом.

Плоский граф— это граф, нарисованный таким образом, что его ребра не пересекаются. Говорят, что граф допускает плоскую укладку, если его можно нарисовать как плоский. Также плоские графы называют планарными.

Граф, изображенный на рисунке 8.1. – плоский.

Существуют и непланарные графы. На рис. показаны два таких графа.

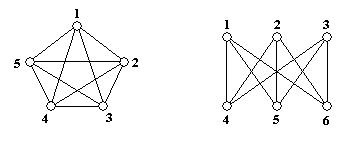
Орграф

Граф называется ориентированным (орграфом), если пары в наборе Х упорядоченные, т.е. для каждого ребра задано направление. Ребра в ориентированном графе называются дугами. В ориентированном графе каждая дуга имеет направление, показанное стрелкой.

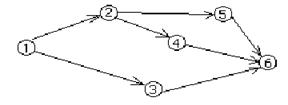
Рис. 8.3. Ориентированный граф.

Маршрут в орграфе называется путем.

В орграфе, изображенном на рис. 8.3 последовательность (v₁, v₃, v₄, v₅) является путем, а последовательность (v₁, v₄, v₂) не является, так как не существует дуги, соединяющей v₄ и v₂.

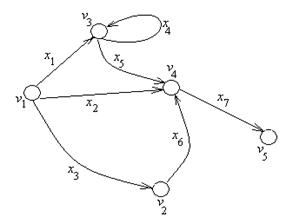
Рисунок 8.4. Ориентированный граф G '=<V ', X '>.

Если вершина является началом дуги, то дуга называется исходящей из вершины, если концом – дуга называется заходящей.

Полустепенью исхода вершины v называется число d^–(v) дуг, исходящих из этой вершины, полустепенью захода – число d⁺(v) дуг, заходящих в вершину.

Для графа, изображенного на рисунке …. d^–(v₁)=3, d⁺(v₁)=0, d^–(v₄)=3, d⁺(v₄)=1.

Связный граф - граф в котором из любой вершины можно найти цепь в любую другую вершину.

Цепь в графе — маршрут, все рёбра которого различны. Если все вершины (а тем самым и рёбра) различны, то такая цепь называется простой (элементарной). В цепи v₀,e₁,...,e_k,v_k вершины v₀ и v_k называются концами цепи. Цепь с концами u и v соединяет вершины u и v. Цепь, соединяющая вершины u и v обозначается <u, v>. Для ориентированных графов цепь называется орцепью.

Граф называется нагруженным, если для его дуг определена весовая функция, задающая «стоимость» пути. «Стоимость» l(x) или l(v_i , v_j) в зависимости от задачи может интерпретироваться как расстояние от пункта i до пункта j, стоимость перевозки, время прохождения данного ребра или дуги x и т. п.

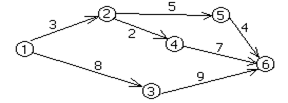
Рис. 8.5. Ориентированный, нагруженный граф G"=<V", X">.

В графе рис. 8.5 для каждой дуги задана некоторая «стоимость» пути. Например, l(1,2)=3. Это означает, что для того, чтобы попасть из пункта 1 в пункт 2 надо потратить 3 часа, или пройти 3 км., или заплатить 3 усл. ден. единицы и т.п.

Эйлеров граф

Эйлеров граф — граф, содержащий эйлеров цикл.

Эйлеров цикл — это эйлеров путь, являющийся циклом.

Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу.

Полуэйлеров граф — граф, содержащий эйлеров путь (цепь).

Существование эйлерова цикла и эйлерова пути.

Разумеется, эйлеров цикл/путь существуют только в связных графах или в графах, которые после удаления всех одиночных вершин превратятся в связные.