Построение низкочастотной части ЛЧХ

В общем случае передаточная функция разомкнутой дискретной системы может быть представлена в виде

.

Рассмотрим построение ЛЧХ для , определяемой непрерывной частью системы, а для D(z) рассмотрим ниже.

Построение будем проводить в функции псевдочастоты l=2/T·tg( 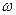T/2) раздельно для области низких частот и для области высоких частот .

Пусть непрерывная часть системы описывается передаточной функцией, соответствующей системе с астатизмом второго порядка

, (1)

С экстраполятором нулевого порядка

Wэ(S)=(1-e^-TS)/s

Примем, что все постоянные времени знаменателя дают сопрягающие частоты меньше чем 2/T ,то есть Ti>T/2 (i=1,2...q). Это предположение приводит к тому, что все изломы асимптотической ЛАХ расположены в низкочастотной области, для которой справедливо неравенство 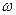T< 2.

Разложим (1) на простые дроби

, (2)

где Ni – коэффициенты разложения;

KT_o = K_W - условная добротность по скорости;

.

На основании результата полученного ранее, можно записать

	Wон (z)=

Z   {KT0/S2}=KT0Tz/(z-1)2

Учитывая, что

где d_i=e^-T/Ti (i=1,2..q),

получим:

Перейдем к дискретной частотной передаточной функции заменой z на w и w=jl^T/₂

В результате получим

Так как было принято, что T_i>T/2 , то

	cth(T/2Ti)=1/tg(T/2Ti) »1/(T/2Ti) =2Ti /T откуда

Сравнение последнего выражения с (2)показывает, что частотные передаточные функции Wон(jl^T/₂) и Wо(j 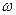) в низкочастотной области совпадают. Так как было принято, что 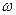T<2, то влияние дополнительного множителя (1-jl^T/₂) в (3)можно не учитывать при построении ЛАХ низкочастотной области.

Совпадение ЛЧХ для дискретной и исходной передаточной функции непрерывной части в области низких частот дает большие удобства в формировании низкочастотной части ЛАХ, проектируемой системы и позволяет использовать методику, изложенную выше для непрерывных систем.

Построение высокочастотной части цифровых систем с экстраполятором нулевого порядка.

Рассмотрим построение логарифмических частотных характеристик в области высоких частот при 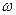>2/T. Введем следующие ограничения.

1. Величина обратная периоду дискретности T, больше половины частоты среза ЛАХ непрерывной части системы, то есть 1/T> /2 или 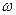_ср<2/T.

Данное неравенство приходится выполнять практически во всех случаях в связи с требованием по устойчивости и запасу устойчивости.

2. Если рассматривать передаточную функцию непрерывной части в виде

где K[с^-r] – общий коэффициент усиления;

r – степень астатизма,

то все постоянные времени T₁..T_n можно разделить на две группы. К первой группе, T₁..T_q отнесем те из них, которым соответствуют сопрягающие частоты меньше 2/T (большие постоянные времени). Они участвуют в формировании низкочастотной части логарифмических характеристик в соответствии с изложенным выше.

Ко второй группе T_q+1..T_n отнесем те постоянные времени, которым соответствуют сопрягающие частоты, большие, чем 2/T (малые постоянные времени), причем для каждой постоянной времени второй группы должно выполняться неравенство

T_i<T/2 (i=q+1,..n)

3.Постоянным времени t₁... t_m соответствуют сопрягающие частоты меньше частоты 2/T, и они участвуют в формировании низкочастотной части ЛАХ, ЛФХ. Это требование не относится к тем постоянным времени числителя, которые были введены для компенсации в непрерывной части некоторых полюсов передаточной функции и поэтому после сокращения одинаковых множителей не вошли в окончательное выражение (1).

4.Пересечение вертикальной прямой 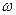=2/T асимптотической ЛАХ непрерывной части происходит при отрицательных наклонах 20дб/дек и 40дб/дек.

Рассмотрим сначала случай, когда пересечение вертикальной линии 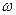=2/T происходит при отрицательном наклоне -20дб/дек. Тогда в области высоких частот ( 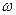=2/T) передаточная функция непрерывной части при отсутствии временного запаздывания может быть представлена в виде

,

где =(Kt₁t₂...t_m)/(T₁T₂...T_q) - представляет собой базовую частоту высокочастотной части ЛАХ, определяемую как частота пересечения ее первой асимптоты с осью нуля децибел. Причем должно выполняться условие

m=q+r-1

В частном случае базовая частота 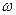_ов может совпадать с частотой среза ЛАХ 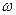_ср. Это будет, например, когда коэффициент усиления для ЛАХ поднят на столько, что ось нуля децибел пересекается последней асимптотой низкочастотной части.

Аналогично предыдущему найдем дискретную передаточную функцию переходом к псевдочастоте по формулам:

W_о (z)=^(z-1)/_z·Z{W₀(s)/s},

z =(1+w)/(1-w),

l=²/_T tg( 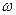^T/ ₂), w=jlT/2.

Учитывая, что

получим в результате

.

Так как Ti<T/2, можно положить .

Учитывая, что SNi= –STi= –T_S получим в результате

.

Это выражение и может быть использовано для построения ЛАХ.

Начало ЛАХ в высокочастотной области сливается с концом ЛАХ в низкочастотной области в точке l=2/T.

W(jl)= K(1+ jlt1)... (1+ jltm) (1- jlT/2)[1+ jl(T/2-TS)] (jl)r (1+ jlT1)... (1+ jlTq) (1+ jlT/2)

Результирующее выражение для дискретной частотной передаточной функции имеет вид

Результирующий фазовый сдвиг равен

	j(l)= -r 90o+ arctg(ltk) - arctg(lTi) - 2arctg(lT/2) +arktg

В результате при построении высокочастотного хвоста ЛАХ приходится учитывать сумму малых постоянных времени T_S и дополнительный множитель

(1-jlT/2). Последний приводит к нулевому наклону ЛАХ и дает дополнительный сдвиг фазы в отрицательную сторону равный arc tg(lT/2).

Если пересечение вертикальной линии 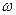=2/T асимптотической ЛАХ непрерывной системы происходит с наклоном –40дб/дек, то в области высоких частот >2/T вместо (2)имеем

Здесь T_S=T_q+1+...T_n

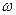_ов²=(Kt₁t₂.. t_m)/(T₁T₂..T_q),причем m=q+r - 2

Переходя к дискретной частотной передаточной функции будем иметь

	W ов(jlT/2)= (1- jlt1)[1/(jl)2 - TS/ jl + ].

Wов(jlT/2)= (1-jlT/2)[1+ jl(T/2-TS)-( jl)2(TTS/2 -Tэ2)] ( jl)2 (1+ jlT/2)

Как и ранее, так как 2T_i<T, можно положить cth(T/2T_i)»1, тогда

Здесь T_э²= T_q+1² +T_q+2² +...+T_n².

Поскольку T_ST/2 > T_э²,

1+jl(T/2- T_S)-( jl)²(T_ST/2- T_э²)»(1+ jlT/2)(1- jlT_S).

Окончательно

.

Это выражение и должно использоваться для построения высокочастотной части ЛАХ и ЛФХ. На частоте l=2/T происходит сопряжение низкочастотной и высокочастотной частей характеристик.

Результирующее выражение для частотной передаточной функции разомкнутой системы, которой можно пользоваться для построения ЛАХ и ЛФХ во всем частотном диапазоне имеет вид

	Wов(jl)= K(1-jlT/2) (1-jlTS)(1+jlt1)...(1+jltm) ( jl)r (1+jlT1)... (1+jlTq)

Фазовый сдвиг для этой передаточной функции равен

	m q j(-l)=-r 90o+Sarctg(ltk)- Sarctg(lTi)- arctg(T/2)- arctg (lTS) k=1 i=1

Особенности построения ЛАХ колебательных звеньев не рассматриваем. При необходимости самостоятельно. В.А.Бесекерский “Динамический синтез САР” М.Наука 1970.