Метод средней скользящей взвешенной

Этапы построения прогноза по временным рядам

1. Предварительный анализ данных;

2. Построение моделей: формирование набора аппроксимирующих функций (кривых роста) и численное оценивание параметров моделей;

3. Проверка адекватности моделей и оценка их точности;

4. Выбор лучшей модели;

5. Расчет точечного и интервального прогнозов.

На этапе предварительного анализа данных производится проверка наличия тренда; сглаживание временных рядов; расчет показателей развития динамики экономических процессов.

Выявление наличия тенденций в развитии исследуемого показателя

Тенденции среднего текущего значения временного ряда визуально можно определить из графика исходных данных. Наличие тенденций среднего уровня на графике становится более заметным, когда на нем отражены сглаженные значения исходных данных.

Процедура сглаживания необходима при построении некоторых математических моделей и для устранения аномальных наблюдений.

Чаще всего для сглаживания применяются методы:

- средней скользящей простой;

- средней скользящей взвешенной;

- экспоненциальное сглаживание.

Самым простым методом сглаживания является

Метод средней скользящей простой

1.1 Сначала для временного ряда 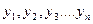определяется интервал сглаживания 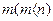. Необходимо при прочих равных условиях интервал сглаживания 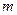брать нечетным;

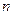– большое число для сглаживания мелких беспорядочных колебаний;

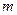– небольшое число, если нужно сохранить более мелкие колебания).

1.2. Для первых 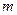уровней временного ряда вычисляется их средняя арифметическая (это будет сглаженное значение уровня ряда, находящегося в середине интервала сглаживания);

1.3. Затем интервал сглаживания сдвигается на один уровень вправо, повторяя вычисление средней арифметической.

Для вычисления сглаженных уровней ряда 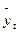применяется формула:

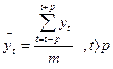
где 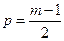(при нечетном ).

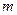В результате такой процедуры получается 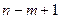сглаженных значений уровней ряда, при этом первые 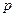и последние 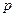уровней ряда теряются (не сглаживаются).

Недостаток метода в том, что он применим лишь для линейных трендов.

Метод средней скользящей взвешенной

Отличие от предыдущего метода в том, что уровни, входящие в интервал сглаживания, суммируются с разными весами. Используется формула средней арифметической взвешенной

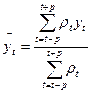
где 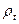- вес 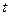-го уровня временного ряда.

При краткосрочном прогнозировании наиболее эффективными оказываются адаптивные модели учитывающие неравномерность уровней временного ряда. Адаптивные модели прогнозирования – это модели дисконтирования данных, способные быстро приспосабливать свою структуру и параметры к изменению условий.

Согласно схеме скользящего среднего, оценкой текущего уровня является взвешенное среднее всех предшествующих уровней, причем веса при наблюдениях убывают по мере удаления от последнего уровня, т.е. информационная ценность наблюдений признается тем большей, чем ближе они к концу интервала наблюдений.