Операции над множествами
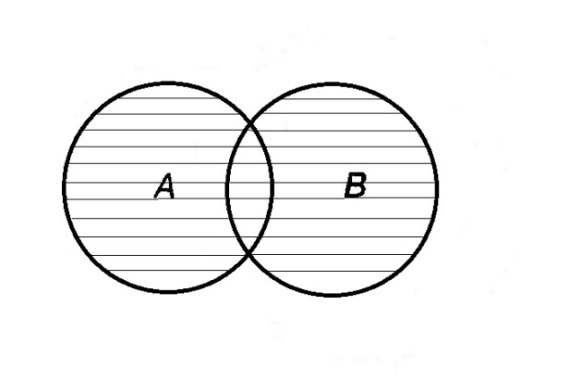
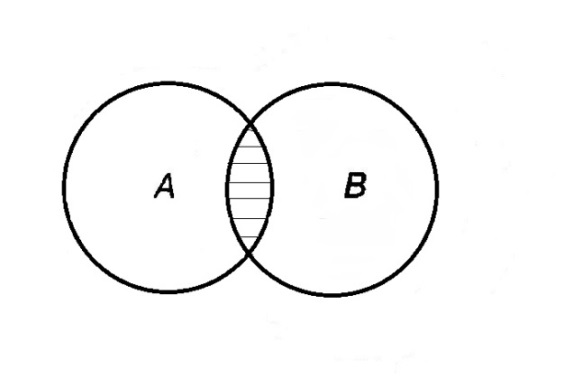
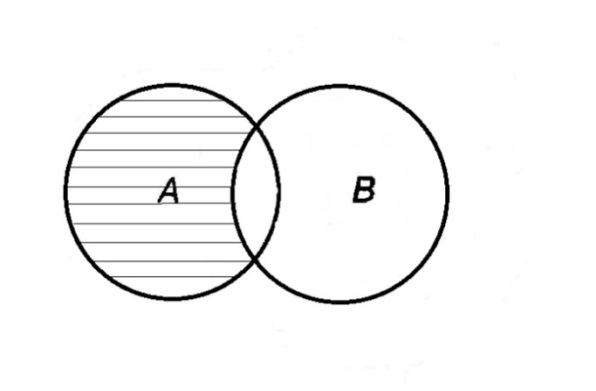
Определение 1.4.Объединением или суммой множеств A и B называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств.
Объединение множеств обозначают A 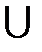 B (или A +B). Кратко можно записать A
B (или A +B). Кратко можно записать A 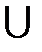 B =
B = 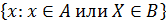 .
.
A 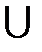 B= A +B
B= A +B
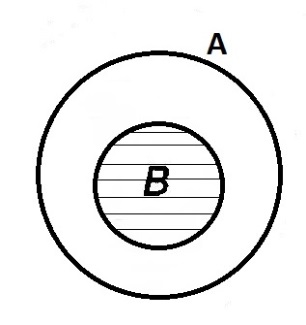
Если B 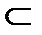 A, то A +B=A
A, то A +B=A
Определение 1.5.Пересечением или произведением множеств A иB называется множество, состоящее из элементов, каждый из которых принадлежит множеству A и множествуBодновременно. Пересечение множеств обозначают A  B (илиA·B). Кратко можно записать:
B (илиA·B). Кратко можно записать:
A  B =
B = 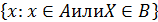 .
.
A  B =A ·B
B =A ·B
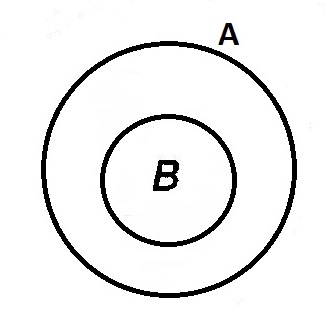
ЕслиB 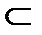 A, тоA · B= B
A, тоA · B= B
Определение 1.6. Разностью множеств A и B называется множество, каждый элемент которого является элементом множества Aи не является элементом множества B. Разность множеств обозначают A/B. По определению A/B = 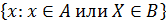 .
.
A/B =A–B
Множества, элементами которых являются числа, называются числовыми.
Примерами числовых множеств являются:
N = 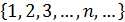 - множество натуральных чисел.
- множество натуральных чисел.
Z= 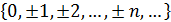 - множество целых чисел.
- множество целых чисел.
Q= 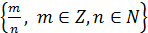 - множество рациональных чисел.
- множество рациональных чисел.
R‒ множество действительных чисел.
Множество R содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью. Так, 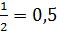 ;
; 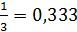 … ‒ рациональные числа.
… ‒ рациональные числа.
Иррациональное число выражается бесконечной непериодической десятичной дробью. Так, 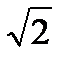 = 1,41421356...;
= 1,41421356...; 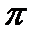 = 3,14159265.... – иррациональное число.
= 3,14159265.... – иррациональное число.
K– множество комплексных чисел (вида Z=a+bi)
R 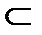 K
K
Определение 1.7.Ɛ ‒ окрестностью точки x0 называется симметричный интервал (x0 – Ɛ; x0 + Ɛ), содержащий точку x0.
В частности, если интервал (x0 –Ɛ; x0 +Ɛ), то выполнятся неравенство x0 –Ɛ<x<x0 +Ɛ, или, что то же, │x– x0 │<Ɛ. Выполнение последнего означает попадание точки x в Ɛ – окрестность точки x0.
Пример 1:
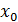 = 2, Ɛ = 0,1.
= 2, Ɛ = 0,1.
(2 – 0,1; 2 + 0,1) или (1,9; 2,1) – Ɛ– окрестность.
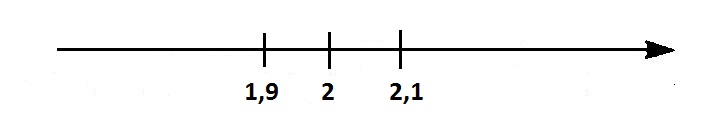
│x– 2│< 0,1
–0,1<x – 2<0,1
2 –0,1<x< 2 + 0,1
1,9<x< 2,1
Пример 2:
A– множество делителей 24;
B– множество делителей 18.
A= 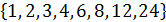 .
.
B= 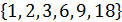 .
.
A 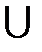 B= A +B =
B= A +B = 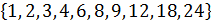
A  B =A ·B =
B =A ·B = 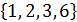
A /B =A –B = 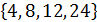
Лекция 2. ФУНКЦИЯ
Понятие функции. Основные свойства функции.
Определение 1. Пусть даны два непустых множестваХ и Y.Соответствие f, при котором каждому элементу x 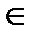 Хсоответствует один единственный элемент у
Хсоответствует один единственный элемент у 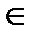 Y, называется функцией и записывается у = f(x),
Y, называется функцией и записывается у = f(x),
x 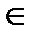 Хили f:x→ у (x → у).
Хили f:x→ у (x → у).
x— аргумент функции; у — значение функции.
Пример:
y = 2 x – 1
| X0 – 1 |
| – 1Y –3 |
Множество Хназывается областью определения функцииfи обозначается D(f). Множество всех у 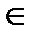 Yназывается множеством значений функцииfи обозначается E(f).
Yназывается множеством значений функцииfи обозначается E(f).
Если элементами множеств Х и Yявляются действительные числа, то функцию fназывают числовой функцией.
