Приложение. Процедура линеаризации

Одним из способов визуализации функциональных зависимостей, делающих их более наглядными, является построение графика зависимости зависимой величины от независимой величины, т.е. такой, которая может быть задана экспериментатором в некотором интервале произвольно. Например, в опыте с математическим маятником независимой величиной является длина маятников, а зависимой – его период Т. Соответствующая теоретическая зависимость имеет вид 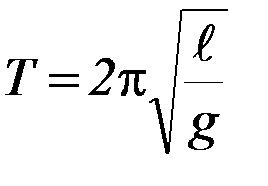. Графики этой зависимости при различных значениях ускорения свободного падения g (оно, как правило, и подлежит определению) – семейство парабол, показанных схематично на рисунке.

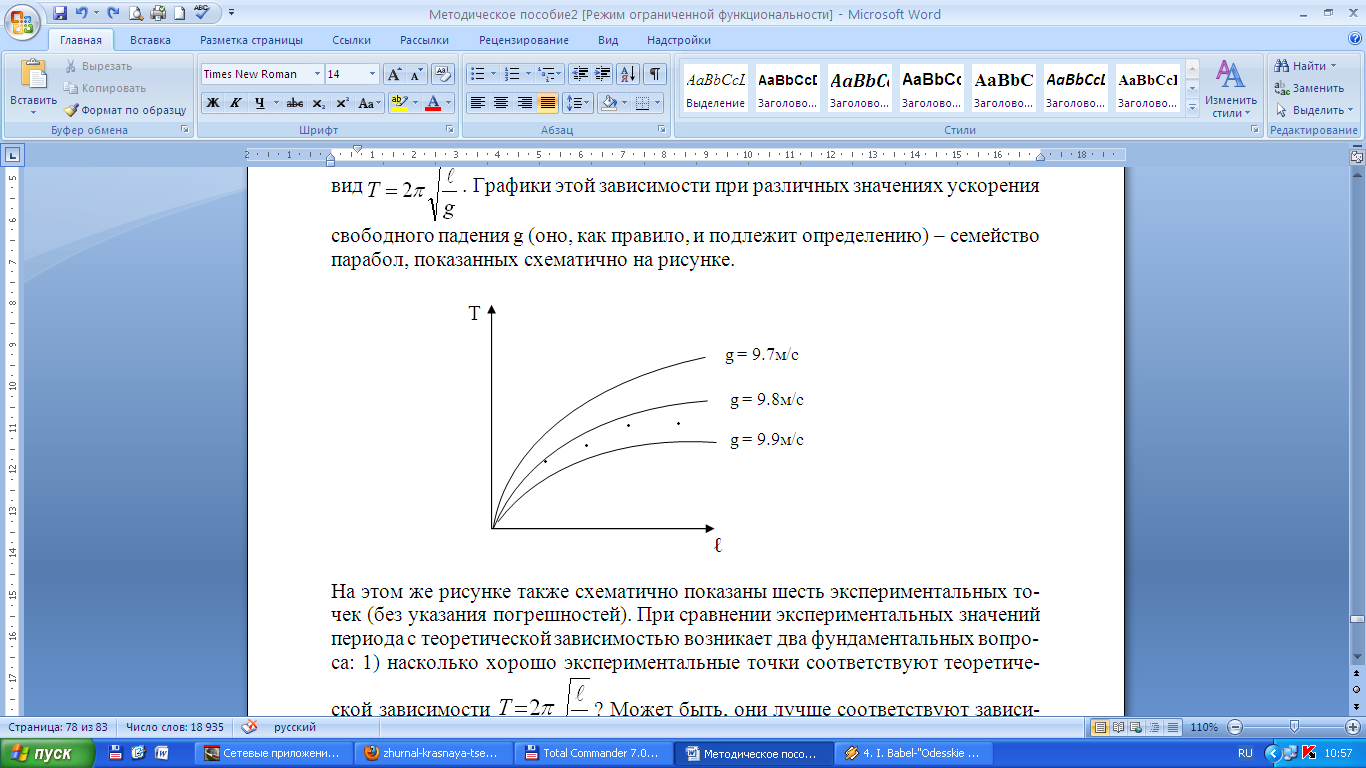
На этом же рисунке также схематично показаны шесть экспериментальных точек (без указания погрешностей). При сравнении экспериментальных значений периода с теоретической зависимостью возникает два фундаментальных вопроса: 1) насколько хорошо экспериментальные точки соответствуют теоретической зависимости 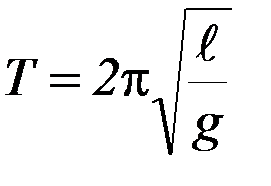? Может быть, они лучше соответствуют зависимости 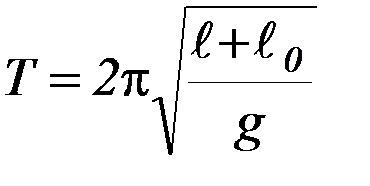, где l₀ – некоторая постоянная длина? 2) Если соответствие экспериментальных точек зависимости 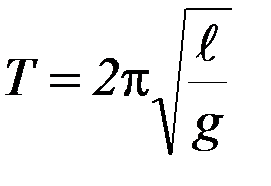хорошее, то как найти значение g, соответствующее экспериментальным – точкам. Графическая визуализация проводится в лабораторном эксперименте для включения в процесс познавательной деятельности человеческого глаза. Лучше всего человеческий глаз оценивает, насколько хорошо экспериментальные точки лежат на теоретической кривой в том случае, когда эта кривая является прямой. Поэтому из зависимой физической величины или из независимой физической величины или из той и другой одновременно образуют конструкции, зависимость между которыми линейна. Соответствующая процедура называется линеаризацией. В данном случае она сводится к следующему.

Возводим выражение для периода в квадрат

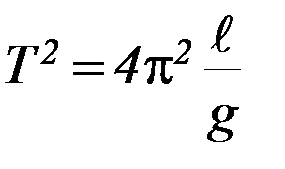или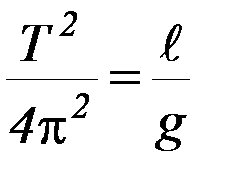

Обозначим 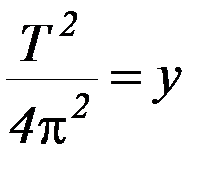, тогда зависимость 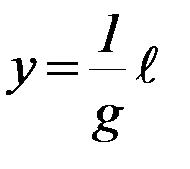– линейная и, следовательно, график теоретической зависимости y(l)– прямая линия, проходящая через начало координат. Если на координатной плоскости (l, y) отметить экспериментальные точки, то визуально легко устанавливается, достаточно ли хорошо расположение экспериментальных точек соответствует линейной зависимости. Прямая, соответствующая экспериментальным точкам наилучшим образом, может быть теоретически найдена с помощью МНК или проведена даже от руки. Процедура линеаризации неоднозначна. Например, можно записать 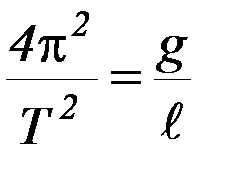. Обозначим 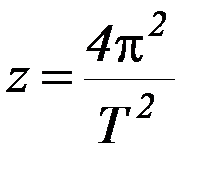, 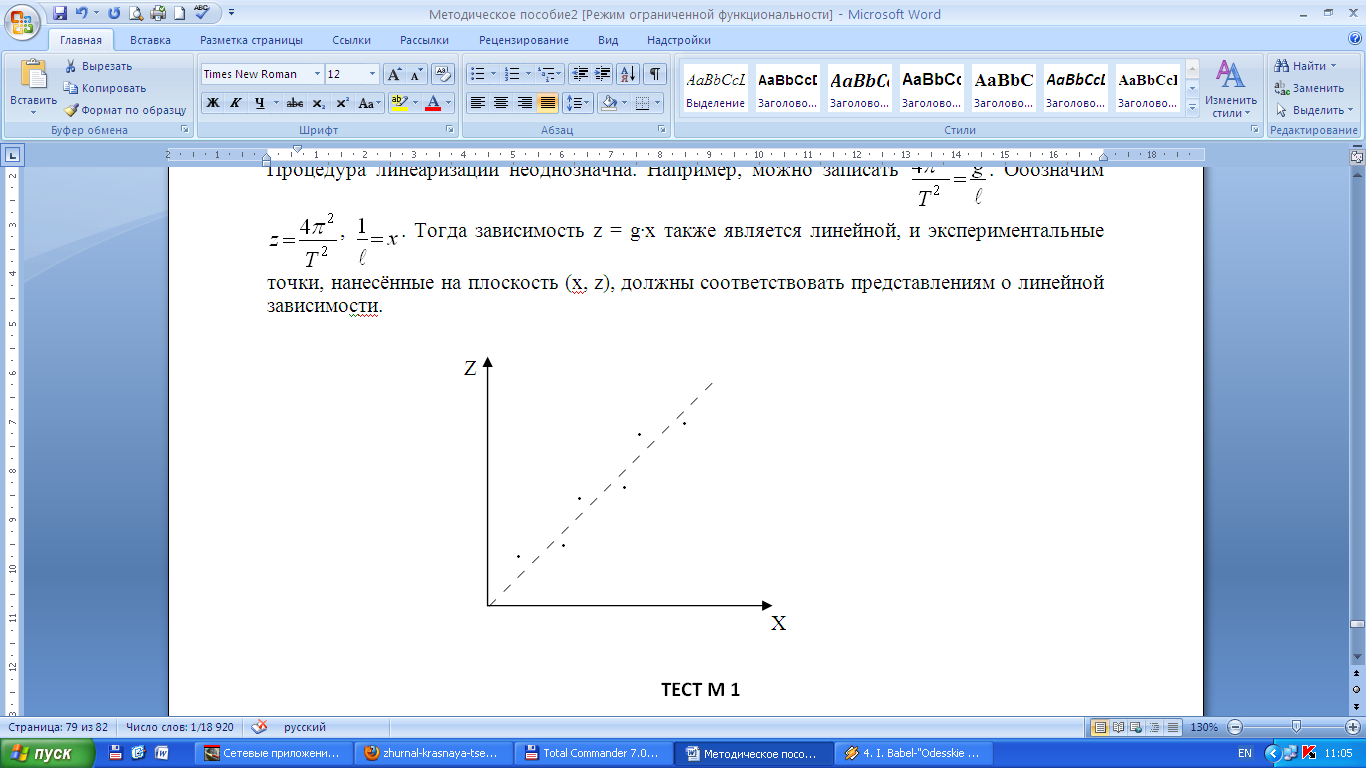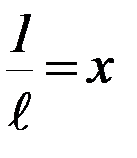. Тогда зависимость z = g·x также является линейной, и экспериментальные точки, нанесённые на плоскость (х, z), должны соответствовать представлениям о линейной зависимоcти.

ТЕСТ М 1

1. Студент измерил длину стола с помощью 20 – сантиметровой линейки с сантиметровыми делениями. Какой из представленных результатов, соответствует стандартам лабораторного физического практикума?

линейка

1) 124 см; 2) 124,0 см; 3) 124,5 см; 4) 124,32 см; 5) 124,3 см

2. В предыдущем измерении погрешность добросовестного студента равна:

3. Относительная погрешность результата добросовестного студента составляет:

4. Размеры стола измерялись 30 – сантиметровой линейкой с миллиметровыми делениями. Принимая в качестве модели стола прямоугольник, запись для его длины и ширины выглядит следующим образом

1245 мм

1249 мм

5. Площадь стола из п.4 равна:

6. Толщина стола из п. 4 равна 15 мм, масса 10,1 кг. Найти плотность материала стола.

7. В результате измерения зависимости от времени координаты х тела получена следующая таблица

t, c
x, м	3,1	5,1	7,0	9,1

Какая из зависимостей лучше соответствует экспериментальным данным в смысле МНК?

1) х = 2,0 t + 3,1 2) x = 2,1 t + 2,9...

8. Уравнение наилучшей в смысле МНК прямой имеет вид:

9. Для кинематического закона движения

x = 3.0 t + 4.0, м y = 4.0 t – 5.0, м

скорость равна:

10. Для кинематического закона движения из п. 9 скорость составляет угол a с осью Х, равный:

11. Для кинематического закона движения

х = 3.0 t y = 10 + 4.0 t – 5.0 t²

уравнение траектории имеет вид:

12. Для закона движения п. 11 скорость в момент падения равна:

13. Для того же закона скорость в момент падения составляет угол с осью Х, равный:

14. Для того же закона движения средняя путевая скорость равна:

15. Для того же закона движения средняя скорость перемещения по модулю равна:

16. Для того же закона движения средняя скорость составляет с осью ОХ угол, равный:

17. Радиус кривизны траектории в точке падения равен:

18. Центр кривизны траектории в точке падения имеет координаты:

19. Кинематический закон движения в некоторой системе координат (X´, Y´) имеет вид: х´ = 8 + 5 t – 4 t² и y´ = 6 – 3 t² ускорение частицы равно при этом:

20. Для того же кинематического закона угол между ускорением и осью X^/ составляет:

21. Для того же кинематического закона начальная скорость равна:

22. Для того же закона начальная скорость составляет с осью X´ угол, равный:

23. На какой угол повёрнута система координат из п. 11 по отношению к системе координат из п. 19?

24. Преобразования от системы координат (X´, Y´) к системе (X, Y) имеют следующий вид:

25. Одно тело движется согласно закону п. 11, а другое, начавшее движение из начала координат одновременно с первым, толкнули вверх вдоль наклонной плоскости с углом наклона a = arccos 0.6 с начальной скоростью 5 м/с. Трения нет. Если со вторым телом связать систему координат (Х, У), оси которой параллельны осям (X, Y), то кинематический закон движения первого тела в системе отсчёта, связанной со вторым, будет иметь вид:

26. Относительная скорость тел в момент падения первого на наклонную плоскость равен:

27. Относительная скорость в указанный в п. 26 момент времени составляет угол с осью X, равный:

Литература

1. Савельев, И.В. Курс общей физики. – М.: Наука, 1982. – Т.1.

2. Детлаф, А.А. Курс физики / А.А. Детлаф, Б.М.Яворский. – М.: Высшая школа, 1989.

3. Зисман, Г.А. Курс общей физики / Г.А.Зисман, Г.А.Тодес. – Киев, Днiпро, 1994.

4. Петровский, Н.Н. Механика. – Минск, Высшая школа, 1969.

Учебное издание

Чопчиц Николай Игнатьевич

Гладыщук Анатолий Антонович

Янусик Ирина Семеновна