Контрольная работа № 1. 2. 1. Даны матрицы
1.
2. 1. Даны матрицы
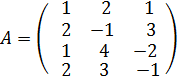и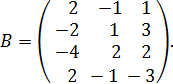 
Определить, имеет ли матрица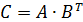 
обратную.
2. Методом обратной матрицы решить систему:
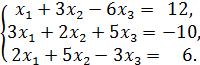
3. Определить, имеет ли однородная система
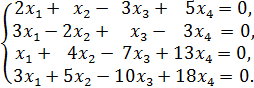
ненулевое решение. Найти общее решение системы.
4. Даны четыре вектора
=(4;5;2); =(3;0;1); =(–1;4;2); =(5;7;8).
в некотором базисе. Показать, что векторы , , образуют базис, и найти координаты вектора в этом базисе.
5. а) Методом Лагранжа привести квадратичную форму
f(x1, x2)=–2x12+6 x22–8x1x2
к каноническому виду (указать пример соответствующего
преобразования координат).
б) По критерию Сильвестра исследовать на
знакоопределенность квадратичную форму
f(x1, x2, x3)=2x12+3x32–2x1x2+4x1x3–8x2x3.
6. Найти координаты вершин углов прямоугольного
треугольника, если его катет и гипотенуза лежат на прямых
и соответственно, а одна из вершин, лежащих
на этом катете, имеет абсциссу, равную 2. Сделать чертеж.
7.Написать уравнение плоскости, проходящей через начало
координат перпендикулярно прямой, проходящей через точки и .
Контрольная работа № 2
1.Найти предел .
2. Написать уравнение касательной к графику функции
в точке с абсциссой, равной 1. Сделать чертеж.
| 3. Исследовать функцию и схематично построить ее график. | |
| 4. Вычислить определенный интеграл: | |
5. Вычислить площадь фигуры, ограниченной линиями
, , . Сделать чертеж.
6.Экспериментальные данные о переменных х и у приведены в
таблице:
| 2,4 | 2,1 | 2,0 | 1,2 | 1,5 |
В результате их выравнивания получена функция
. Используя метод наименьших квадратов,
аппроксимировать эти данные линейной зависимостью
(найти параметры а и b). Выяснить, какая из двух линий лучше (в
смысле метода наименьших квадратов) выравнивает
экспериментальные данные. Сделать чертеж.
7.Решить задачу Коши:
; .
8. Исследовать сходимость ряда
Примеры выполнения заданий контрольных работ
Ниже приведены (с решениями) типовые варианты контрольных работ по дисциплине «Высшая математика».
Эти варианты составлены из соответствующих задач с решениями учебников [1 или 5], практикумов [2 или 6], учебника [3] или учебника [4], номера которых представлены в таблице.
Решения задач типовых вариантов
| № зада-ния | Номера задач (с решениями) | |||||||||||
| по учебникам [1] или [5] | по практикумам [2] или [6] | по учебнику[3] | по учебнику [4] - к.раб. № 1 по учебнику [5] - к.раб. № 2 | |||||||||
| Контрольная работа № 1 | ||||||||||||
| 1.13 | 1.50 | 1.15 | 1.15 | |||||||||
| 2.1 | 2.1 | 2.1 | 2.1 | |||||||||
| 2.4 | 2.35 | 2.4 | 2.4 | |||||||||
| 3.4 | 3.24 | 3.39 | 3.44 | |||||||||
| 3.7 | 3.71 | 3.7 | 3.12 | |||||||||
| 4.5 | 4.5 | 4.5 | 4.5 | |||||||||
| ‒ | 4.88 | 4.109 | 4.109 | |||||||||
| Контрольная работа № 2 | ||||||||||||
| 6.11и | 6.68 | 6.11г | 2.11г | |||||||||
| 7.15б | 7.109а | 7.105 б | 3.105б | |||||||||
| 8.14 | 8.96 | 8.112 | 4.112 | |||||||||
| 11.18б | 11.1в | 11.23г | 7.23г | |||||||||
| 11.21 | 11.30в | 11.56в | 7.56в | |||||||||
| 15.13 | 15.88 | 9.101 | 5.101 | |||||||||
| 12.13 | 12.45 | 12.73 | 8.76 | |||||||||
| 13.14д | 13.15г | 13.32б | 9.32б | |||||||||
ЛИТЕРАТУРА
Основная[2]
1. Высшая математика для экономистов. Учебник /под ред. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2010.
2. Высшая математика для экономистов. Практикум /под ред. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2010.
3. Высшая математика для экономического бакалавриата. Учебник и практикум / под ред. Н.Ш. Кремера.– М.: Юрайт, 2014.
4. Кремер Н.Ш., Фридман М.Н. Линейная алгебра. Учебник и практикум / под ред. Н.Ш. Кремера.– М.: Юрайт, 2014.
5. Кремер Н.Ш., Путко Б.А., Тришин И.М. Математический анализ: Учебник и Практикум / под. ред. Н.Ш. Кремера – М.: Юрайт, 2014.
6. Математика для экономистов и менеджеров. Учебник /под ред. Н.Ш. Кремера. – М.: Кнорус, 2015.
7. Математика для экономистов и менеджеров. Практикум /под ред. Н.Ш. Кремера. – М.: Кнорус, 2015.
Дополнительная
8. Кремер Н.Ш., Путко Б.А., Тришин И.М. Математика для экономистов: от Арифметики до Эконометрики. Учебно-справочное пособие / под ред. Н.Ш. Кремера.– М.: Юрайт, 2014.
9. Солодовников А.С., Бабайцев В.А., Браилов А.В., И.Г.Шандра Математика в экономике. – М: Финансы и статистика, ИНФРА-М, 2011, ч. 1,2.
10. Сборник задач по курсу "Математика в экономике". Под ред. В.А. Бабайцева, В.Б. Гисина.— М. : Финансы и статистика: Инфра-М, 2010.
11. Ахтямов А.М. Математика для социологов и экономистов. Учебное пособие. – М.: Физматлит, 2006.
12. Красс М.С., Математика для экономического бакалавриата. ‒М.ИНФРА-М, 2011
13. Малугин В.А. Линейная алгебра. – М.: РидГрупп, 2011.
14. Малугин В.А. Математика для экономистов. Математический анализ. Курс лекций. – М.: Эксмо, 2009.
15. Ильин В.А., Позняк Э.Г. Линейная алгебра. М.: Физматлит, 2005.
16. Ильин В.А., Позняк Э.Г. Основы математического анализа. В 2-х ч. ‒. М.: Физматлит, 2009.
Электронные ресурсы
1. Линейная алгебра. Обзорная лекция для студентов I курса всех направлений (http://repository.vzfei.ru).
2. Математический анализ. Обзорная лекция для студентов I курса всех направлений (http://repository.vzfei.ru).
3. Компьютерная обучающая программа для студентов 1 курса по дисциплине «Математика» (КОПР1-М); зарегистрирована в Информационно-библиотечном фонде РФ, рег. №50200000053 от 08.06.2000. Дата обновления 06.12.2010. (http://repository.vzfei.ru). Доступ по логину и паролю.
4. Высшая математика. Учебно-методическое пособие /под ред. Н.Ш. Кремера – М., 2015 (электронная версия в разделе «Образовательные ресурсы» на сайте «Финансовый университет – заочное обучение»).(http://repository.vzfei.ru).
5. И.М Эйсымонт, Н.Ш. Кремер. Математический анализ и линейная алгебра. Методические указания по компьютерному тестированию – М.: Вузовский учебник, 2007 (электронная версия в разделе «Учебные ресурсы» на портале Финуниверситета) (http://repository.vzfei.ru).
6. Н.Ш. Кремер, И.М Эйсымонт. Математика. Методические указания по проведению и выполнению контрольных работ с частичным использованием КОПР – М.: ВЗФЭИ, 2009 (электронная версия в разделе «Учебные ресурсы» на портале Финуниверситета)(http://repository.vzfei.ru).
7. Электронная библиотека (www.bibliotekar.ru ).
Содержание
Предисловие……………………………………………………………… …3
Введение ........................................................................................................5
Основные правила приближенных вычислений.....................................7
Содержание дисциплины и методические рекомендации по
ее изучению …………………………….……………………………………10
Часть 1. Линейная алгебра…………………………………………………10
Раздел I. Элементы матричного анализа……………………..………10
Тема 1.Матрицы и определители………………………………………...10
Тема 2. Системы линейных уравнений………………………………….12
Тема 3. Векторные пространства…….…………………………………. 15
Тема 4. Линейные операторы………………………………………........ 16
Тема 5. Квадратичные формы………………………………………… 17
Раздел II. Элементы аналитической геометрии………………………18
Тема 6. Элементы аналитической геометрии…..………….…………... 18
Часть 2. Математический анализ………………………………………….21
Раздел III. Введение в анализ……………………………………………21
Тема 7. Функция………………………………………………………..…21
Тема 8. Пределы и непрерывность………………………………........ 22
Раздел IV. Дифференциальное исчисление………………………… .24
Тема 9. Производная………………………………………………..... 24
Тема 10. Приложения производной……………………………….... ..25
Тема 11. Дифференциал функции…………………………………....... .26
Тема 12. Функции нескольких переменных.............................................26