Математическое описание модели

1. Рассеяние данного выходного параметра X станка подчиняется закону нормального распределения с характеристиками области состояний

a₀ = X_1ср – математическое ожидание;

σ_a = σ₁ – среднеквадратическое отклонение.

2. Изменение выходных параметров во времени подчиняется линейному закону:

,

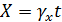где γ_x – скорость изменения параметра (γ_x = const для данного сочетания внешних факторов).

3. Рассеяние скоростей изменения параметров подчиняется нормальному закону распределения с характеристиками:

γ_{x ср} – математическое ожидание;

σ_x – среднеквадратическое отклонение;

γ_x – случайная величина, и на ее рассеяние действуют различные факторы: нагрузка, скорость, смазка и ее загрязненность и т.д.

4. Изменение выходных параметров станка при износе через промежуток времени t, характеризующие закон нормального распределения:

γ_xt – математическое ожидание;

σ_xt – среднеквадратическое отклонение.

5. Выход области состояний за пределы области работоспособности (X_max) приведет к параметрическому отказу.

Как известно, вероятность отказа F(t) численно равна площади кривой f(X), находящейся за пределами X_max, а вероятность безотказной работы P(t) численно равна площади кривой f(X), находящейся в области работоспособности. Эту площадь определим, пользуясь функцией Лапласа Ф:

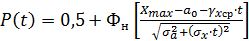, (3.1)

где .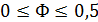

Вероятность отказа .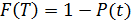

6. Формула (3.1) позволяет определить вероятность безотказной работы для каждого выходного параметра. Вероятность безотказной работы всего станка определим следующим образом:

.

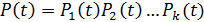7. Задаваясь рядом значений t, можно построить зависимость P(t) в функции времени:

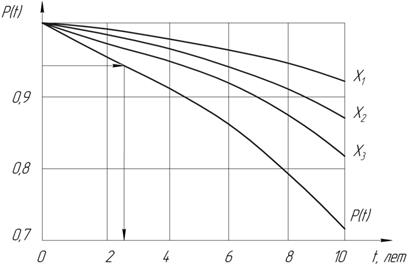
Рисунок 3.3. Вероятность безотказной работы

ЗАКЛЮЧЕНИЕ

Для повышения безотказности машин и их элементов применяются следующие основные методы:

1. Повышение надежности узлов и элементов благодаря рациональной конструкции и применению износостойких материалов. Большая сопротивляемость вредным воздействиям на узел уменьшает скорость потери его работоспособности и смещает кривую рассеивания сроков службы f(t) в область более высоких значений t и повышают вероятность безотказной работы за данный период времени.

2. Повышение стабильности технологических процессов при изготовлении деталей машин. Это приводит к уменьшению дисперсии сроков службы, что даже при одинаковых сроках службы может повысить надежность элементов F₁ < F_2.

3. Обкатка машины и ее узлов позволяет выявить те недостатки изготовления и сборки, которые приводят к повышенным внезапным отказам в первый период работы машины (время t₁ желательно исключать из времени работы машины).

4. Защита машины от случайных перегрузок или вредных воздействий.

5. Применение резервирования для систем из элементов невысокой надежности.

6. Применение самовосстанавливающихся схем.

7. Упрощение системы. Создать более простую машину, выполняющую заданную ранее функцию.

ПРИЛОЖЕНИЕ

ЗАДАНИЕ 1

По значениям ординат опорных точек траектории перемещения суппорта токарного станка рассчитать изменения этих траекторий в функ­ции времени:

а) заданы величины износа 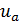, , 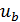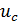(мкм) передней и задней направляю­щих станины (Табл. 1);

б) определить суммарное изменение радиуса обработанной детали:

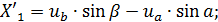
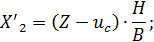
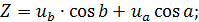
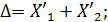
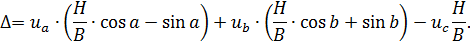
В) определить изменения ординат опорных точек направляющих скольже­ния в функции времени для каждого выходного параметра

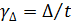, мкм/год,

где t= 1;3;5;10 лет.

ВАРИАНТЫ ЗАДАНИЯ 1

Таблица 1

Величины износа 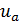, , 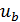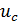(мкм)

передней и задней направляю­щих станины

Вариант	Износ направляющих, мкм	Выходные параметры	Геометрические характеристики направляющих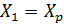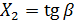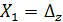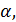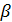
			град.	, град.	Н/В
	Ua	0,3	0,4	0,35			0,6
	Ub	0,4	0,45	0,5
	Uc	0,9	0,85	1,0
2	Ua	0,8	0,85	0,7			0,8
	Ub	0,4	0,6	0,5
	Uc	2,0	1,0	1,2
	Ua	0,25	0,3	0,45			1,0
	Ub	0,65	0,5	0,3
	Uc	2,0	1,0	0,8
	Ua	1,0	0,8	0,94			2,0
	Ub	0,65	0,5	0,92
	Uc	0,95	0,8	0,95
	Ua	0,6	0,55	0,35			0.6
	Ub	0,45	0,7	0,4
	Uc	0,5	0,8	0,95
	Ua	0,35	0,4	0,6			1,0
	Ub	0,65	0,85	0,35
	Uc	0,8	1,0	0,9
	Ua	0,55	0,5	0,7			0,6
	Ub	0,25	0,3	0,45
	Uc	0,4	0,6	0,8
	Ua	0,3	0,35	0,4			1,0
	Ub	0.25	0,35	0,8
	Uc	0.2	0,3	0,4
	Ua	0,3	0,5	0.45			0,8
	Ub	0,45	0,5	0,6
	Uc	0,5	0,9	0,85
	Ua	0,45	0,35	0,5			1,0
	Ub	0,6	0,5	0,8
	Uc	0,85	0,75	1,0
	Ua	0,2	0,3	0,4				0,6
	Ub	0,8	0,75	0,8
	Uc	0.75	0,8	1,0
		Ua	0,2	0,3	0,4			0,8
		Ub	0,4	0,5	0,4
		Uc	1,2	1,0	0,8
		Ua	0,8	0,75	0,8			1,0
		Ub	0,65	0,6	0,75
		Uc	0,75	0,8	1,0
		Ua	0,5	0,65	0,7			0,8
		Ub	0,6	0,7	0,7
		Uc	1,0	2,0	1,0
		Ua	0,5	0,6	1,0			1,0
		Ub	0,65	0,7	2,0
		Uc	0,7	0,7	1,0
		Ua	0,8	0,65	0,75			1,0
		Ub	0,75	0,6	0,8
		Uc	0,8	0,75	1,0
		Ua	0,2	0,4	1,2			0,6
		Ub	0.3	0,5	1,0
		Uc	0,4	0,4	0,8
		Ua	0,45	0,65	0,90			1,0
		Ub	0,35	0,50	0,75
		Uc	0,5	0,8	1,0
		Ua	0,3	0,45	0,5			0.8
		Ub	0,5	0,5	0,9
		Uc	0,45	0,6	0,85
		Ua	0,3	0,25	0,2			1,0
		Ub	0,35	0,35	0,3
		Uc	0,4	0,8	0,4
		Ua	0,55	0,25	0,4			0,6
		Ub	0,5	0,3	0,6
		Uc	0,7	0,45	0,8
		Ua	0,35	0,65	0,8			1,0
		Ub	0,4	0,85	1,0
		Uc	0,6	0,35	0,9
		Ua	0,6	0,45	0,5			0,6
		Ub	0,55	0,7	0,8
		Uc	0,35	0,4	0,95
		Ua	0,1	0,65	0,95			2,0
		Ub	0,8	0,5	0,8
		Uc	0,94	0,92	0,95
		Ua	0,25	0,65	2,0			1,0
		Ub	0,3	0,5	1,0
		Uc	0,45	0,3	0,8

ЗАДАНИЕ 2

1. Рассчитать рассеяние скоростей изменения параметров X₁, X₂, X₃:

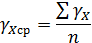
и среднеквадратическое отклонение

,

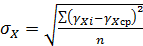где i – индекс максимального значения γ_x.

2. Рассчитать вероятность безотказной работы станка (область работоспособности)

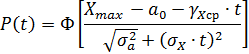
для каждого выходного параметра.

3. Рассчитать вероятность безотказной работы станка

P(t) = P₁(t)·P₂(t)·P₃(t)

при t = 1; 3; 5; 10 лет.

4. Построить зависимость P(t) в функции времени.

5. Определить ресурс T_p станка по точности при P(t) = 0,95.

6. Сделать выводы.

7. Результаты расчетов сведем в таблицу 2.

Таблица 2

Оценка параметрической надежности станка

Вы ход ной   пара метр	Область состоя ний по результатам   испыта ний	Область работо способ ности   Xmax, мкм	Заъпас   надежно сти   кн	Результаты   прогноза   и расчета	Расчет   вероятности P(t)   при работе станка     t, лет	Средний ресурс по пара метру   Tср, лет
	a0 = x1 ср	σa = σ1			γx ср, мкм/год	σх, мкм/год	1 год	3 года	5 лет	10 лет
x1	Данные из табл. 1 (практ. №1)
x2
x3
Показатели параметрической надежности станка	Вероятность безотказной работы P(t)					Средний ресурс станка Тср
	Ресурс по точности Tp при P(t) = 0,95

СПИСОК ЛИТЕРАТУРЫ

1. Б.М. Бржозовский А.А. Игнатьев В.В. Мартынов и др. Диагностика и надежность автоматизированных систем. - Учебное пособие (гриф МОРФ). - Старый Оскол: ТНТ, 2011. - 352 с.

2. Схиртладзе А. Г. Технологическое оборудование машиностроительных предприятий [Текст] : учебное пособие / А. Г. Схиртладзе, Т. Н. Иванова, В. П. Борискин. - 2-е изд., перераб. и доп. - Старый Оскол : ТНТ, 2012. - 168 с. - ISBN 978-5-94178-124-9 : Гриф: УМО АМ.

3. Металлорежущие станки [Текст] : учебник / В. Д. Ефремов [и др.] ; под общ. ред. П. И. Ящерицына. - 5-е изд., перераб. и доп. - Старый Оскол : ТНТ, 2009. - 696 с. - ISBN 978-5-94178-129-4 : Гриф УМО АМ.

4. Проников А.С. Программный метод испытания металлорежущих станков. М.: Машиностроение, 1995. 287с.

5. Старков В.К. Обработка резанием. Управление стабильностью и качеством в автоматизированном производстве. М.: Машиностроение, 1989. 295 с.

6. Старков В.К. Технологические методы повышения надежности обработки на станках с ЧПУ. М.: Машиностроение, 1994. 119 с.

7. Пляскин И.И. Оптимизация технологических решений в машиностроении. М.: Машиностроение, 1992. 175 с.

8. Шенк Х. Теория инженерного эксперимента. М.: Изд-во «Мир», 1982. 381 с.