Ключи к тестам для самоконтроля
| № теста | |||||||||||||||
| № Ответа | г | в | а | а | б | а | в | б | в | б | а | в | а | в | а |
| № теста | |||||||||||||||
| № ответа | а | в | б | а | г | б | а | в | а | г | б | в | а | а | б |
| № теста | |||||||||||||||
| № ответа | г | г | в | а | а | а | г | б | б | а | а | г | в | а | а |
| № теста | |||||
| № ответа | в | г | б | в | б |
Образец и решение типового варианта теста
Вариант №***
1.Кривая смертей задана формулой 
. Функция выживания 
равна
1) 
2) 
3) 
4) 
Решение.
Функция выживания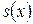 
через функцию плотности (кривую смертей) 
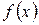определяется по формуле
.
Тогда 
[интегрируя по частям]= 
.
Ответ: 2)
2.Время жизни некоторого конкретного человека в возрасте 30 лет описывается законом де Муавра с предельным возрастом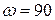 
лет. Вероятность того, что этот человек проживет еще 10 лет и умрет на протяжении последующих 5 лет, равна
1) 
2) 
3) 
4) 
Решение.
Вероятность того, что человек возраста 
лет проживет еще 
лет и умрет на протяжении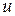 
последующих лет равна
.
Функция выживания 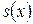в модели Муавра с предельным возрастом 
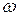имеет вид
.
Тогда 
.
Ответ: 3)
3. Страхователь в возрасте 40 лет заключил договор страхования жизни сроком на 5 года (норма доходности – 5%, страховая сумма – 100000 руб., доля нагрузки – 9%). Ежегодная брутто-премия, вычисленная через коммутационные числа, равна
1) 1397,3
2) 1535,5
3) 1721,5
4) 1940,8
Решение.
Ежегодная нетто-ставка (НС) при страховании жизни сроком на 
лет, вычисленная через коммутационные числа (коммутационные функции) на единицу страховой суммы, равна
,
где 
– коммутационные числа (находят по таблице коммутационных чисел).
Брутто-ставка (БС) с долей нагрузки 
равна 
, а брутто-премия (БП) со страховой суммой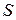 
– 
.
Тогда получим 
,
(руб).
Ответ: 2)
4. Время жизни описывается моделью де Муавра с предельным возрастом 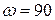лет, а эффективная процентная ставка 
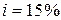. Человек в возрасте 50 лет заключил договор страхования жизни сроком на 10 лет. Единовременная нетто-ставка для этого человека в процентах (%) равна
1) 7,855
2) 9,743
3) 11,625
4) 13,466
Решение.
Остаточное время жизни застрахованного имеет равномерное распределение на промежутке 
:
Интенсивность процентов 
, коэффициент дисконтирования 
.
Единовременная нетто-ставка при страховании жизни сроком на лет равна
.
Тогда 
Ответ: 4)
5. Мужчина в возрасте 40 лет покупает за 100000 рублей пожизненную ренту (пенсию), выплаты которой начинаются с возраста 65 лет. Эффективная процентная ставка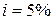 
. Величина ежегодных выплат равна
1) 159236
2) 121550
3) 89189
4) 75620
Решение.
Величина ежегодных выплат 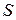равна
,
где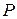 
– стоимость пожизненной ренты,
– отложенная на 
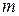лет пожизненная рента для человека возраста лет, выраженная через коммутационные числа 
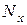и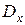 
(эти числа находят по таблице коммутационных чисел).
Тогда 
,
.
Ответ: 3)
Вопросы к зачету
1. Время жизни как случайная величина.
2. Свойства функции выживания.
3. Кривая смертей, интенсивность смертности. Свойства.
4. Аналитические законы смертности (Мэйкхама, Вейбулла, Гомперца).
5. Макрохарактеристики продолжительности жизни.
6. Остаточное время жизни. Распределение остаточного времени жизни.
7. Основные величины, связанные с остаточным временем жизни.
8. Округленное время жизни. Распределения округленного времени жизни.
9. Приближения для дробных возрастов (равномерное, постоянная интенсивность смертности, Балдуччи).
10. Макрохарактеристики остаточного времени жизни.
11. Частичная остаточная продолжительности жизни.
12. Анализ индивидуальных убытков при краткосрочном страховании жизни.
13. Приближенный расчет вероятности разорения.
14. Принципы назначения страховых премий.
15. Общая модель долгосрочного страхования жизни.
16. Теорема о дисперсии приведенной ценности.
17. Связь между непрерывными и дискретными видами страхования.
18. Перестрахование: сущность и разновидности договоров перестрахования.
19. Пропорциональное перестрахование. Перестрахование превышения потерь.
20. Пожизненные ренты, выплачиваемые раз в год.
21. Пожизненные ренты, выплачиваемые с частотой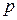 
.
22. Периодические нетто-премии.