Формализация решения задачи векторным методом

Как отмечали, критерий выбора решения на каждом этапе определяется двумя параметрами – длиной вектора решения и величиной угла вектора решения с идеальным вектором (n=0). Соответственно свести задачу к однокритериальной, можно рассматривая длину проекции вектора решения на идеальный |x_no| = x_n cosa_no

Если обозначить через x_n1 = 1,n параметры n-ого варианта, то длина вектора равна: x_n =

_m

[∑x²_ni] ^1/2

ⁱ⁼¹

Ортонормируем систему следующим образом. Примем x_ni= x_ni / x_oi, i=1,n

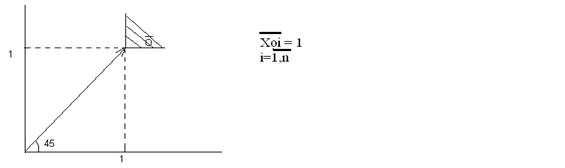
_m

Получим длину проекции в ортонормированном базисе. x_no =(1/√m) ∑ x_ni

ⁱ⁼¹

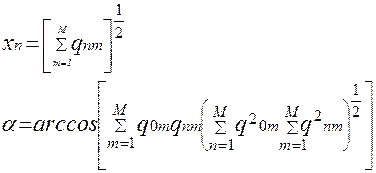Замечание. Длина вектора и угол между векторами определяются по следующим формулам:

Данное выражение после соответствующих подстановок, в предположении, что нормированное значение идеального вектора равно 1: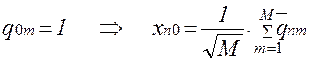

Так как значение m фиксировано для всех вариантов решения, это значение можно опустить, таким образом, в качестве критерия выбора оптимального вектора, на каждом шаге, можно рассматривать параметр, определяемый следующим выражением:

_m

x_no = ∑ x_ni

ⁱ⁼¹ (6)

x_ni = x_ni / x_oi

Видим, что эти формулы просты, что позволяет эффективно использовать данный метод решения задачи ЛП с использованием вычислительных средств.

Таким образом, методика выбора оптимального решения сводится к следующему:

1. на каждом шаге используем критерий (6) , выбирается лучшее значение исходя из

_m

x_no = ∑ x_ni → max

ⁱ⁼¹

1. с учетом выбранного вектора (что соответствует его откладыванию в системе координат) изменяем систему ограничений (вычитаем из ограничений соответствующие параметры векторов).
2. проверяем все полученные ограничения на условие ≤ 0. если для всех ограничений оно выполняется, задача решается. Если условие не выполняется возвращаемся к шагу 1, с перенормированием значений параметров.

Пример: вернемся к задаче раскроя материала, рассмотренной ранее.

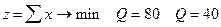
Способ
Раскрой первого типа
Раскрой второго типа

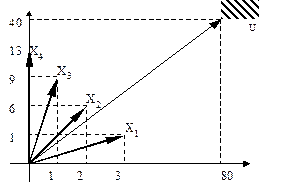
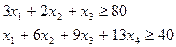
Для иллюстрации выполним несколько шагов решения задачи.

Шаг 1. Считаем значения критерия для различных вариантов.

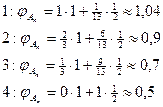
Сравниваем – выбираем лучший вариант – это вариант1 (присваиваем х₁ = 1).

Формируем новые ограничения: 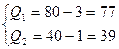. Задача не решена, следовательно, требуется следующий шаг решения (не все ограничения нулевые). Следующий шаг отличается от предыдущего тем, что в аддитивном критерии изменяется.

Шаг 22. Рассчитываем значение критерия 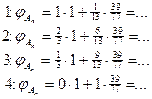. И так далее (выбираем лучшее значение по данному критерию, фиксируем отложенный х, пересчитываем ограничения, проверяем, решена ли задача полностью или требуется следующий шаг решения). И т.д.