Обработка результатов косвенных измерений
Плотность параллелепипеда определяется, согласно формуле:
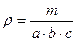 | (17) |
Определить абсолютную и относительную погрешности плотности параллелепипеда.
1. Определить частные абсолютные погрешности:
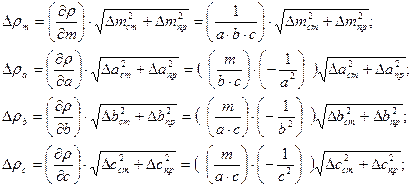 | (18) |
2. Определить полную абсолютную погрешность:
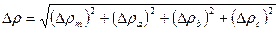 | (19) |
3. Находятся границы доверительного интервала (погрешность результата измерений)
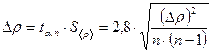 | (20) |
где 2,8 – коэффициент Стьюдента, определяется из табл. 1 (α = 0,95, n = 4)
4. Оценивается относительная погрешность результата серии измерений
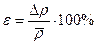 | (21) |
5. Окончательный результат, запишется в виде ρ=ρ± Δρ (кг/м3).
Значение погрешности следует округлять до двух значащих цифр, если первая является единицей и до одной значащей цифры во всех остальных случаях. Для записи измеренного значения последней записывается цифра того десятичного ряда, который содержит погрешность (см. табл. 2).
Т аблица 2. Примеры записи результата
| Правильно: | Неправильно: | Ошибка: |
| 1,2 ± 0,2 | 1,244 ± 0,2 | Лишние цифры в значении результата |
| 1,24 ± 0,03 | 1,2438 ± 0,0325 | Лишние цифры в значении погрешности |
| 1,244 ± 0,014 | 1,244 ± 0,01 | Грубое округление погрешности |
| 1,24 ± 0,03 | 1,24 ± 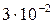 | Множитель 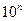 должен быть общим должен быть общим |
Точность расчетов
Если число записывается в виде десятичной дроби, то одним из источников погрешностей вычислений является округление числа. В качестве погрешности округления принимается половина единицы последнего, указанного после округления результата. Мерой точности числа является число значащих цифр. Значащими цифрами называются все цифры, кроме левых нулей (которые служат для указания разрядов). Именно число значащих цифр определяет относительную погрешность. Примеры определения погрешностей округления некоторых чисел приведены в табл. 3.
Таблица 3.Примеры определения погрешностей округления некоторых чисел
| Пример | Число значимых чисел | Погрешность округления |
| 3,1416 | ± 0,00005 | |
| 1,24 ± 0,03 | ± 0,005 | |
| 1,244 ± 0,014 | ± 0,00005 | |
| 1,24 ± 0,03 | ± 0,0005 |
Число значащих цифр в промежуточных расчетах должно быть на единицу больше, чем в результатах измерений. В противном случае погрешность округления (т.е. расчетов) будет сравнима с погрешностью измерений. Табличные данные следует также брать с достаточным числом значащих цифр (если это возможно), либо учитывать погрешности округления этих данных.
1.6. Погрешности приборов
В учебных лабораториях отсчеты со шкалы приборов снимаются, как правило, с точностью до целого деления. Допустим, что при повторных измерениях в показаниях прибора нет разброса в значениях результатов. В этом случае ошибка измерения оценивается как погрешность однократного измерения, определяемая максимальной погрешностью прибора DХпр.
Механические приборы (линейка, штангенциркуль, микрометр и т. д.) имеют инструментальную погрешность DХпр, равную половине цены деления шкалы: DХпр = с/2, где с – цена деления.
Для технических весов моделей ВЛТ – 1 кг, Т – 1000 с диапазоном измерений 50…1000 г, используемых в учебных лабораториях кафедры физики, предельная абсолютная погрешность (по паспорту): DХвес = 100 мг.
Набор гирь 4-го класса с диапазоном измерений (10 мг ... 1110 г), применяемых в учебных лабораториях кафедры, содержит гири со следующим допустимым отклонением от номинальных значений масс (из паспортных данных): 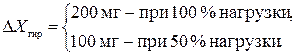
Погрешность определения массы при взвешивании складывается из погрешности весов и погрешности гирь: 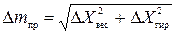 .
.
Для электроизмерительных стрелочных приборов (амперметр, вольтметр и т. д.)
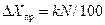 , , | (22) |
где k – выраженный в процентах класс точности, который указывается на шкале прибора.
Например, 0,05; 0,1; 0,2 – образцовые приборы, 0,5; 1,0 – лабораторные приборы, 1,5; 2,5; 4,0 – технические приборы. Если класс точности на приборе не указан, то он считается равным 4,0. В формуле (22) N – максимальное показание прибора (диапазон всей шкалы). Для приборов с двухсторонней шкалой или со шкалой, начинающейся не от нуля, под N следует понимать полный интервал изменения измеряемой величины.
Из выражения (22) следует, что абсолютная погрешность электроизмерительных приборов не меняется при переходе от начала к концу шкалы, однако, относительная ошибка при этом резко уменьшается. Отсюда вытекает важная рекомендация: выбирать прибор (или шкалу многопредельного прибора) следует так, чтобы стрелка прибора при измерениях заходила за середину шкалы.
Для цифровых электроизмерительных приборов, получивших в настоящее время широкое распространение, пределы допускаемых значений погрешности измерений следует брать из паспортных данных приборов. При отсутствии этих данных для грубой оценки можно полагать, что максимальная погрешность равна единице разряда последней значащей цифры на рабочем диапазоне прибора.
Для осциллографов погрешности измерения амплитуды (напряжений) исследуемых сигналов, а также погрешности измерения временных интервалов указываются в техническом описании приборов. При отсутствии этих описаний для грубой оценки можно считать, что одно маленькое деление шкалы приблизительно равно максимальной погрешности осциллографа на данном диапазоне измерений.
Основные метрологические характеристики приборов (диапазон измерений, цена деления, класс точности, погрешность) заносятся в метрологическую таблицу. При этом для многопредельных приборов (цифровых электроизмерительных, осциллографов и т.д.) в колонке «диапазон измерений» указываются:
1. Общий диапазон измерений, который в свою очередь сам содержит несколько диапазонов;
2. Рабочие диапазоны измерений, т. е. те, которые были выбраны студентом при проведении измерений.
При отсутствии паспортных данных таких приборов, как осциллографы, генераторы сигналов и т. д., в качестве грубой оценки ΔХпр можно принять одно деление шкалы на рабочем диапазоне измерений.
