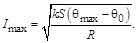Процесс описания объектов моделирования

Построение математических моделей

Процесс описания объектов моделирования

Моделирование как основной научный метод в начальной стадии своего развития был главным образом предметом искусства исследователя. Процесс построения моделей определялся теоретическим багажом исследователя, его неформальными представлениями о цели работы, опытом, экспериментаторским мастерством и интуицией.

Вместе с тем опыт модельных исследований все более сложных объектов убедительно показывал, что качество модели и особенно трудоемкость ее создания решающим образом зависят от того, сколь целесообразно организован процесс изучения объекта, построения, проверки и практического использования его модельного описания. Возникла задача оптимизации процесса моделирования.

Наибольшее развитие методика и практика планирования и осуществления модельных исследований получили в рамках таких направлений, как исследование операций и прикладной системный анализ.

В сложных случаях, когда невозможно составить модели с помощью известных теоретических представлений, получили развитие экспериментальные исследования, названные идентификацией объектов. Применительно к этим исследованиям зародилась и стала стремительно развиваться теория оптимального планирования эксперимента, обеспечивающая получение необходимой экспериментальной информации об объекте при минимальной затрате сил и средств.

В модельном исследовании можно выделить основные этапы: постановку задачи, построение модели, отыскание решения, проверку модели и оценку решения, внедрение модели и контроль ее правильности.

Рассмотрим процесс модельного исследования с помощью его графического представления в форме блок-схемы (рис. 4.1).

Постановка задачи следует за выявлением некоторых противоречий и возникновением проблемы: потребности изменить в лучшую сторону существующее положение вещей в той или иной области.

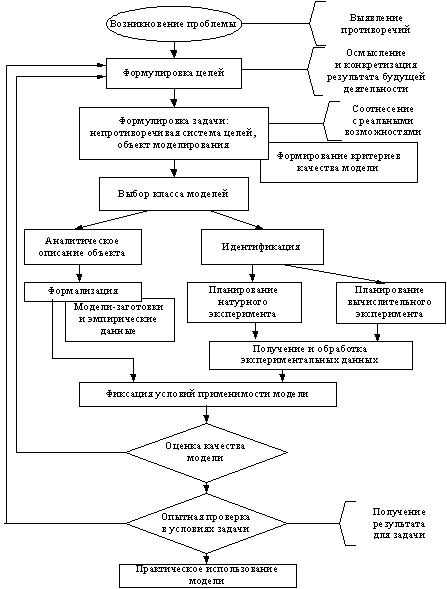
Рис. 4.1. Схема формирования модели

Так, огромное большинство технических и технологических проблем формируется в сфере экономики и экологии – верхних по отношению к технике уровнях системы природа–общество.

Осмысление и конкретизация проблемы приводят к формулировке целей или системы целей как желательного результата будущей деятельности по решению проблемы. Однако поставленная цель, естественно, должна быть соотнесена с реальными возможностями ее достижения или, иными словами, с ресурсами (материальными и другими), которые могут быть использованы для решения данной проблемы. Сопоставление первоначально намеченных целей с ресурсными ограничениями (обычно приводящими к корректировке первых в сторону их сужения) приводит к формулировке задачи исследования, которая помимо непротиворечивой системы целей, учитывающих ресурсные возможности, включает в себя объект моделирования.

Данные о целях исследования, уточненные в формулировке задачи, а также исходная информация об объекте моделирования служат для определения критерия качества создаваемой модели – количественной меры степени ее совершенства. При традиционной постановке задачи исследования критерий обычно не носит формального характера и представляет собой некоторую систему количественных требований, которым должна отвечать будущая модель. В случае вполне формализованной оптимизационной постановки критерий приобретает вид некоторого функционала от переменных и параметров модели, значение которого достигает экстремума при оптимальных ее характеристиках (например, среднеквадратическая погрешность модельных переменных).

Следующим шагом в построении модели является основанный на априорных данных содержательный анализ системы и выбор класса, или точнее, способа формирования модели. Если объект не слишком сложен, достаточно изучен и комплекс подлежащих модельному исследованию свойств и характеристик объекта может быть выявлен на основе теоретических представлений и данных (дополняемых необходимым объемом эмпирической информации), то целесообразно избрать аналитический путь построения модели. Однако на практике часто оказывается, что из-за сложности, слабой изученности объекта или отсутствия соответствующих теоретических разработок (например, применительно к комплексным системам, содержащим технические, информационные, биологические компоненты) этот путь не может быть реализован. Альтернативным является путь идентификации объекта, т. е. экспериментального определения существенных для решаемой задачи свойств и характеристик объекта специально ради построения его модели. Эксперимент, как правило, достаточно сложный и трудоемкий, осуществляется в соответствии со специально разрабатываемым оптимальным планом, данные эксперимента обрабатываются и становятся основой для формализованного описания объекта в виде математической модели вход–выход.

Формализованная модель, построенная теоретическим путем или идентифицированная, оценивается в соответствии с выбранным ранее критерием и либо признается удовлетворительной (принимается), либо отвергается как недостаточно совершенная. В последнем случае возникает необходимость в ее корректировке и итеративном обращении к ранее выполненным этапам.

Решение о принятии модели (в общем случае после i-го итерационного цикла) влечет за собой переход к следующему этапу – опытной проверке непосредственно в условиях той задачи, для решения которой она построена. При этом нередко возникают дополнительные требования (например, связанные с удобством использования модели) и необходимость ее дополнительной корректировки.

Наконец, следует заключительный этап процесса: использование модели по ее прямому назначению – для решения задачи, причем и на этом этапе возможны дальнейшие уточнения и корректировки.

Остановимся на наиболее важных особенностях процесса моделирования в целом.

1. Построение модели представляет собой не однократный акт, а процесс последовательных приближений, в основе которого лежит самообучение исследователя.

2. Процесс моделирования соединяет в себе требования к ясно понимаемому существу решаемой задачи, с одной стороны, и активному владению теорией, математическим аппаратом и методами – с другой стороны. Кроме того, необходимы хорошие знания возможностей вычислительной техники и ее использования.

3. Процесс построения модели является познавательной деятельностью и представляет собой важнейшую составную часть решения задачи в целом.

4.2. Аналитический метод построения
математических моделей

В распоряжении исследователя, решающего на основе моделирования конкретную задачу, сегодня находится огромное множество моделей-«заготовок», которые могут и должны быть использованы. Все эти заготовки получены на основе универсальных законов, таких, как закон сохранения вещества и энергии, начала термодинамики, закон всемирного тяготения. Однако вопрос о том, каким может быть удельный вес теоретической составляющей при построении каждой конкретной модели, целиком определяется требованиями задачи и характером объекта моделирования.

Возможность и рациональность теоретического подхода к моделированию некоторого объекта определяются целым рядом практически не поддающихся формальному анализу факторов, к числу которых относятся:

· степень изученности данного класса объектов и наличие теоретической базы, достаточной для модельного описания объекта в соответствии с требованиями решаемой задачи;

· приемлемость ограничений и допущений, содержащихся в исходных теоретических построениях, применительно к условиям и требованиям решаемой задачи;

· специфические свойства объекта-оригинала (степень сложности и размерность модели, возможность линеаризации, возможность и удобство применения стандартных, например частотных, методов для исследования модели объекта и т. п.);

· возможность и удобство введения в теоретическую модель необходимой дополнительной информации, получаемой опытным путем;

· возможность экспериментального исследования объекта-ориги-нала.

В основе аналитических моделей, как правило, лежат балансовые соотношения, связывающие входные и выходные переменные. Эти соотношения представляют собой частные проявления законов сохранения вещества и энергии.

Пример 1. В простейшей ЭЭС генератор электрической станции Г (рис. 4.2) работает с мощностью P_Г, которая посредством линии электропередачи передается на шины нагрузки, где установлен электродвигатель Д.
В такой ЭЭС при неизменной частоте сохраняется баланс активной мощности:

,

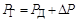где P_д – мощность, с которой работает электродвигатель;

DP – потери мощности в линии электропередачи.

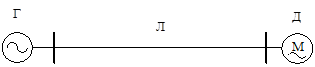
Рис. 4.2. Схема простейшей ЭЭС

Выражение (4.1) является балансовым соотношением, вытекающим из закона сохранения энергии, однако для полного описания модели работы ЭЭС требуются дополнительные экспериментальные данные. К ним относятся характеристики элементов, входящих в ЭЭС: генератора, линии электропередачи и двигателя. Эти элементы являются техническими объектами со своими, свойственными только им, характеристиками. Для получения этих характеристик требуется эксперимент, который проводится непосредственно для этих объектов, либо используются данные экспериментов, выполненные над типичными объектами. К характеристикам электрических объектов относятся, например, статические характеристики генераторов и двигателей по напряжению, а для линии электропередачи – зависимость потерь мощности от напряжения.

Пример 2. При протекании тока по проводу воздушной ЛЭП в соответствии с законом Джоуля–Ленца происходит нагревание проводника:

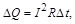
где ΔQ – количество теплоты, выделяемое в проводнике с сопротивлением R при протекании по нему тока I в течение времени Δt.

Если бы не было отвода тепла от проводника, температура проводника возрастала бы неограниченно. Охлаждение проводника происходит лучеиспусканием, конвекцией и теплопередачей из-за наличия теплопроводности окружающей среды.

По условиям сохранения физико-механических характеристик проводов воздушных линий электропередачи температура, до которой могут нагреваться провода, ограничена некоторым значением (как правило 70 ºС). Это связано с ограничением тока, протекающего по проводу I_доп. Вычислить значение I_доп позволяет математическое соотношение, выведенное из баланса количества теплоты, создаваемого в отрезке проводника, и отведенного количества теплоты в единицу времени.

Лучеиспускание при θ < 100 ºС незначительно, а теплопроводность окружающего проводник воздуха мала, следовательно, в основном охлаждение идет за счет конвекции воздуха:

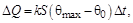
где S – поверхность проводника;

θ_max и θ₀ – максимальная и начальная температура провода;

k – коэффициент пропорциональности.

Приравняем количество создаваемой и количество отводимой теплоты, получим

,

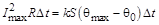откуда