Методы решения нестационарных задач
Обратимся к рассмотренным выше аппроксимациям нестационарных задач. Так, для краевой задачи
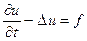 в
в 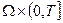 ,
, 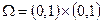 ,
,
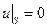 ,
, 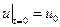 в
в 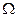
явная разностная схема имеет вид
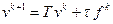 ,
, 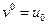 , (2.47)
, (2.47)
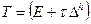 .
.
В чем состоит метод решения системы сеточных уравнений (2.47) – в проведении вычислений по простым рекуррентным формулам.
Неявную разностную схему для рассматриваемой задачи можно записать в виде
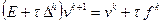 ,
, 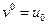 . (2.48)
. (2.48)
Таким образом, для реализации шага неявной схемы следует решить систему сеточных уравнений вида
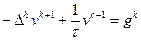 . (2.49)
. (2.49)
Для решения этих систем линейных алгебраических уравнений можно применять различные методы: прямые – метод Гаусса и его различные модификации; итерационные.
Если область, для которой решается задача, является прямоугольником, то существуют специфические весьма эффективные методы решения системы (2.49): прямые методы – быстрое дискретное преобразование Фурье, метод циклической редукции; итерационные методы – метод переменных направлений с оптимальным выбором параметров, метод Р.П. Федоренко, или многосеточный метод (multigrid) и др.
Для довольно широкого класса задач существуют такие схемы, которые сочетают в себе достоинства явных и неявных схем: простота реализации шага почти как для явной схемы, устойчивость при любом соотношении шагов как для неявной схемы.
Продемонстрируем построение этих схем на примере следующей задачи:
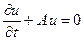 в
в 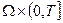 ,
,
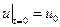 в
в 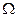 .
.
Предположим, что оператор 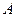 не зависит от времени. Здесь мы считаем, что оператор
не зависит от времени. Здесь мы считаем, что оператор 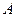 рассматривается на функциях, удовлетворяющих краевым условиям.
рассматривается на функциях, удовлетворяющих краевым условиям.
Относительно оператора 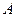 предположим, что
предположим, что
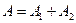 .
.
Предположим также, что решение систем сеточных уравнений, матрицами которых являются соответствующие сеточные операторы 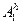 и
и 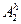 , легко осуществляется и не требует больших вычислительных затрат.
, легко осуществляется и не требует больших вычислительных затрат.
В этом случае удобно рассмотреть следующую схему:
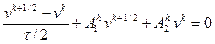 ,
,
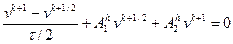 ,
, 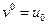 .
.
Это схема переменных направлений, или продольно-поперечная схема. Происхождение названия схемы становится понятным, если применить ее к решению задачи
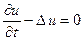 в
в 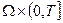 ,
,
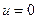 на
на 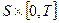 ,
,
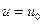 в
в 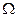 при
при 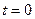 .
.
Для данной задачи схема примет вид
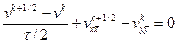 ,
, 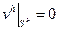 ,
,
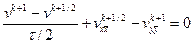 ,
, 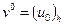 .
.
В первом из этих уравнений схема является явной по направлению переменной 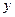 и неявной по направлению переменной
и неявной по направлению переменной 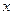 , а во втором уравнении – наоборот.
, а во втором уравнении – наоборот.
Еще одним примером широко используемых схем для решения эволюционных задач являются схемы, которые получаются так называемым методом расщепления.
Приведем пример схемы, полученной методом расщепления:
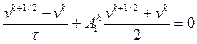 ,
,
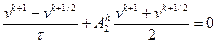 ,
, 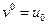 .
.
Для рассмотренного примера, где 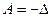 , имеем
, имеем
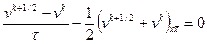 ,
,
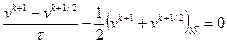 ,
, 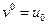 .
.
У этой схемы много названий: локально-одномерная, дробных шагов, покоординатного расщепления.
Обе рассмотренные схемы при 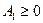 и
и 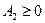 абсолютно устойчивы.
абсолютно устойчивы.
