Функция двух переменных

Если каждой упорядоченной паре чисел (x, y) из некоторой области D (x, y) соответствует единственное число Z, то Z называют функцией двух переменных x и y, x и y – независимые переменные или аргументы, D – область определения функции Z , пишут .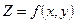

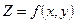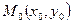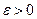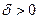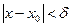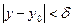Определение: Число B называют пределом функции в точке , если для любого существует , такое, что при всех x и y, удовлетворяющих условиям и , справедливо неравенство 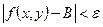. Пишут .

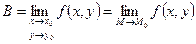Определение:Частной производной по переменной x функции 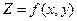называют предел отношения: 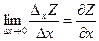, a по переменной y – 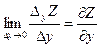; где ,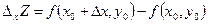

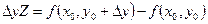. Обозначают , , , .

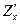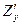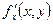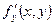Задача. Для функции 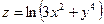найти частные производные функции.

;

.

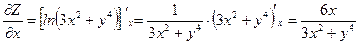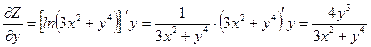Частные производные второго порядка функции 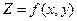имеют вид:

;

;

;

.

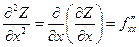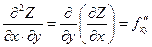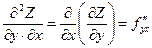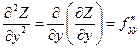Задача.Найти частные производные второго порядка функции .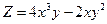

Решение: .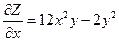

,

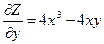
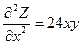
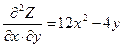
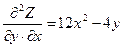
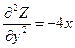очевидно, что = .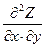

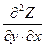Теорема (необходимое условие экстремума): Если точка 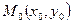является точкой экстремума функции 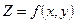, то 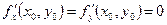или хотя бы одна из них не существует. Точки, для которых это условие выполняется, называются стационарными.

Теорема (достаточное условие экстремума): Пусть 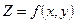имеет непрерывные частные производные до третьего порядка в области, содержащей стационарную точку 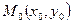. Тогда:

1) если 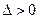, то 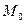– является точкой экстремума, причем если А < 0 (С < 0), то 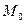– точка максимума, если А > 0 (С > 0), то 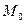– точка минимума;

2) если 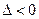, то в точке 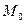нет экстремума;

3) если 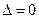, то экстремум может быть, а может и не быть. Необходимо дополнительно исследовать функцию.

Где 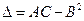, , 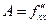, 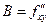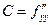в точке .

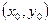Задача.Исследовать функцию 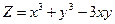на экстремум.

1) Найдем стационарные точки 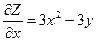, 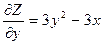. Пользуясь необходимыми условиями экстремума, найдем стационарные точки:

,

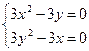откуда .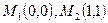

2) Исследуем точк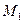и и 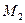, для этого составим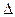

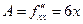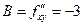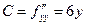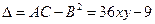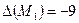, , , . , так как 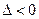, то в точке 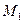нет экстремума. 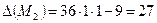, так как 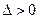и А > 0, то точка 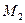– точка минимума. 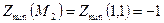, (А = 6 > 0).

Вопросы для контроля

1. Определители второго и третьего порядка.

2. Правила вычисления определителя третьего порядка: разложение по строке (по столбцу), Саррюса, треугольника.

3. Решение систем трех линейных уравнений методом Крамера.

4. Матрицы и действия над ними. Ранг матрицы.

5. Обратная матрица. Решение систем трех линейных уравнений с тремя неизвестными матричным способом.

6. Теорема Кронекера – Капелли. Решение произвольной системы линейных уравнений.

7. Скалярные и векторные величины. Задание вектора в координатной форме. Модуль вектора.

8. Скалярное произведение векторов. Его свойства.

9. Угол между векторами. Условия ортогональности и коллинеарности двух векторов.

10. Векторное произведение векторов и его свойства.

11. Смешанное произведение векторов.

12. Прямая на плоскости. Ее различные уравнения.

13. Взаимное расположение двух прямых на плоскости.

14. Кривые второго порядка: эллипс – вывод канонического уравнения.

15. Гипербола. Вывод канонического уравнения.

16. Парабола. Вывод канонического уравнения.

17. Плоскость в пространстве.

18. Взаимное расположение двух плоскостей.

19. Прямая в пространстве, способы задания прямой.

20. Взаимное расположение двух прямых в пространстве.

21. Взаимное расположение прямой и плоскости.

22. Поверхности второго порядка: сфера, цилиндрические поверхности, конические уравнения поверхностей второго порядка.

23. Функция. Определение, область определения, множество значений.

24. Способы задания. Основные элементарные функции, их графики.

25. Основные классы функций.

26. Числовая последовательность. Предел последовательности.

27. Предел функции в точке и на промежутке.

28. Бесконечно малые и бесконечно большие функции. Эквивалентные бесконечно малые.

29. Раскрытие неопределенностей вида , , .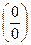

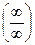30. Первый и второй замечательные пределы.

31. Непрерывность функции в точке и на промежутке.

32. Классификация точек разрыва.

33. Связь предела функции в этой точке с непрерывностью функции.

34. Производная функции. Геометрический смысл.

35. Таблица производных. Правила нахождения производных функций.

36. Дифференциал. Правила дифференцирования.

37. Приложения производных и решение задач. Уравнения касательной и нормали к кривой в точке.

38. Основные теоремы дифференциального исчисления функции одной переменной: Ферма, Ролля, Лагранжа и Коши.

39. Правило Лопиталя.

40. Исследование функции с помощью производной.

41. Функции нескольких переменных. Область определения, график.

42. Предел функции двух переменных. Непрерывность функции двух переменных.

43. Частные приращения и производные.

44. Экстремумы функции двух переменных.