Лабораторная работа № 12
Тема: Приближенное решение обыкновенных дифференциальных уравнений.
Задача Коши.
Задание: Найти приближенные значения решения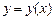 
обыкновенного дифференциального уравнения (ОДУ) 
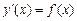на отрезке 
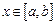с шагом 
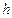при начальном условии 
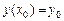используя
d)метод Эйлера;
e)усовершенствованный метод ломаных;
f)метод Эйлера-Коши;
g)метод Эйлера с уточнением;
h)метод Рунге-Кутта четвертого порядка.
Для тестовых примеров найти относительные погрешности и сравнить полученные результаты. Построить графики точного и численного решений.
Оценить погрешность приближенного решения заданного уравнения в выбранной точке, построить график численного решения.
Вопросы самоконтроля.
Постановка задачи Коши для обыкновенных дифференциальных уравнений (ОДУ). Геометрическая иллюстрация.
Основные положения метода Эйлера. Геометрическая интерпретация.
Основные положения метода Эйлера-Коши. Геометрическая интерпретация.
Основные положения метода Эйлера с уточнением. Геометрическая интерпретация.
Метод Рунге-Кутта. Оценка погрешности метода на шаге. Какой метод является более точным, какой менее точным?
| Вариант | |  | | |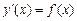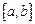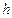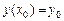
 |  |  |  | |
 | | | | |
 |  | |  | |
 |  |  |  | |
 |  |  |  | |
 | | |  | |
 | | | | |
 | | | | |
| |  |  |  | |
 |  | |  | |
 | | |  | |
 | | |  | |
 |  |  |  | |
 |  | |  | |
 |  | | | |
 | | | | |
 |  |  |  |
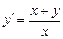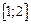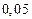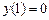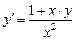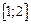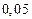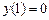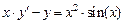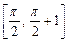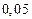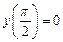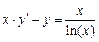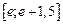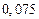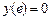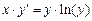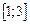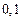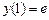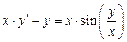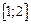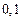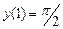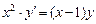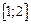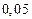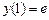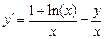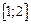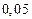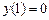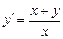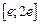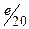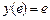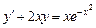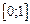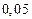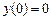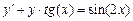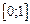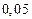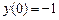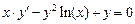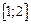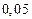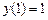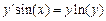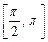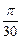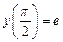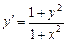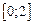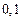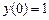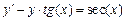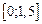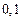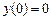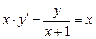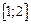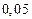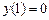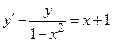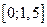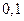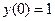Образец выполнения лабораторной работы №12
(Приближенное решение обыкновенных дифференциальных уравнений)
Лабораторная работа № 13
Тема: Численное решение системы ОДУ. Задача Коши.
Задание: 1) Привести ОДУ второго порядка к системе ОДУ первого порядка.
2) Полученную систему численно решить методами Эйлера и Рунге-Кутта с точностью до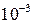 
.
3) Построить график полученного решения и оценить погрешность.
Пример. Дано ОДУ второго порядка
, 
, 
, 
.
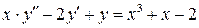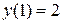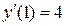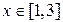Приведем данное ДУ второго порядка к системе ОДУ первого порядка. Для этого введем обозначения: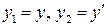 
, тогда получим
, 
, .
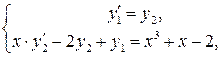
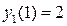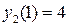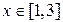Полученная система численно решается методами Эйлера и Рунге-Кутта, строится график функции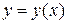 
, оценивается погрешность результата.
Варианты лабораторных заданий
, 
, 
, 
;
, 
, 
, ;
, , 
, ;
, , , ;
, , , ;
, 
, 
, 
;
, 
, , ;
, 
, 
, ;
, 
, , ;
, 
, 
, ;
, 
, 
, ;
, , 
, ;
, 
, 
, ;
, , , ;
, 
, 
, 
, , 
, ;
, 
, 
, ;
, , , ;
, 
,
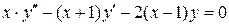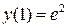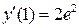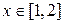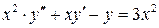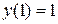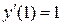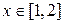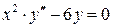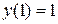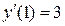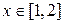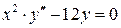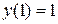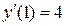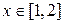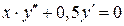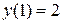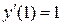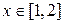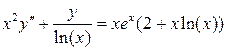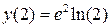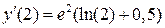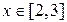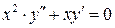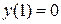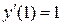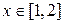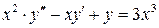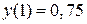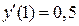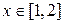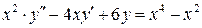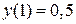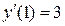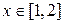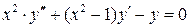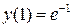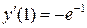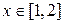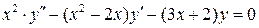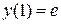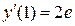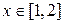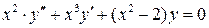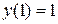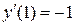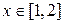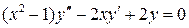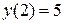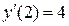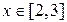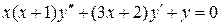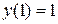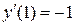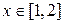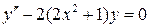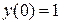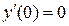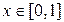
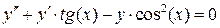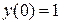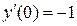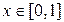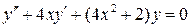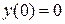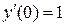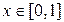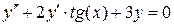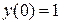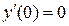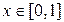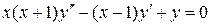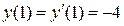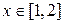
Образец выполнения лабораторной работы №13
(Численное решение системы ОДУ)
Лабораторная работа № 14
Тема: Приближенные методы решения ОДУ. Краевые задачи.
Задание: Из (А) гл.9 Работа №7, стр. 159-161. Проверить соблюдение граничных условий.
Вопросы самоконтроля.
Постановка краевой задачи.
Основные положения метода прогонки (левой, правой, центральной).
На основе какого соотношения ищется приближенное решение ОДУ методом прогонки?
Основные условия применимости метода прогонки.
Оценка погрешности решения ОДУ данным методом.
Образец выполнения лабораторной работы №14
(Приближенные методы решения ОДУ)