Э л е м е н т ы т е о р и и м н о ж е с т в

Московский государственный университет культуры и искусств

Кафедра прикладной информатики

В.С. Колосов

Математика

Учебное пособие для специальности

Культурология

Москва 2012

ББК 22.1

К 61

Рекомендовано к изданию Редакционно-издательским советом МГУКИ

Рецензенты

Макаров В.Л.академик РАН д-р физ.-мат. наук,

Белоцерковский А.С.канд. техн. наук.

Колосов В.С. Математика:Учебное пособие.–М.:

МГУКИ, 2012. – 67 с.

© Московский государственный университет

культуры и искусств, 2012 © Колосов В.С.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 5

Словарь символьных обозначений 9

ЧАСТЬ 1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ 10

1.1. Предыстория 11

1.2. Основные понятия и способы задания множеств 13

1.3. Операции над множествами 17

Практикум 21

Задачи для самостоятельного решения 25

Вопросы для самопроверки 26

ЧАСТЬ 2. ТЕОРИЯ ВЕРОЯТНОСТЕЙ 27

2.1. Предмет теории вероятностей 28

2.2. Основные понятия и определения 29

2.3. Статистический анализ результатов экспериментов 30

2.4. Множество событий и операции на нем 31

2.5. Эмпирическая вероятность 35

2.6. Классическая вероятность 36

2.7. Схемы случайных экспериментов 39

2.7.1. Схема без возвращения с упорядочением 39

2.7.2. Схема без возвращения и без упорядочения 41

2.7.3. Схема с возвращением и с упорядочением 42

2.7.4. Схема с возвращением без упорядочения 42

2.8. Геометрическая вероятность 44

2.9. Условная вероятность 48

2.10. Формула полной вероятности 52

2.11. Формула Байеса 54

Практикум 56

Операции над событиями 56

Расчет числа исходов 57

Классическая вероятность 59

Условная вероятность 61

Формулы полной вероятности и Байеса 61

Задачи для самостоятельного решения 64

Вопросы для самопроверки 65

Рубежный контроль 66

Контрольная 66

Словарь символьных обозначений 67

Список литературы 67

ВВЕДЕНИЕ

Для многих поступающих в гуманитарный вуз заветная мечта – поскорее забыть математику как страшный сон и никогда с ней больше не встречаться. Объяснением тому служат гуманитарные наклонности и накопившееся еще в школе непонимание предмета. Однако Государственный образовательный стандарт предъявляет серьезные требования к математической подготовке будущих специалистов вне зависимости от профиля вуза,

т.к. эта наука является важной составной частью общечеловеческой культуры. Уважительное отношение к ней зародилось еще во время древней Эллады благодаря трудам Пифагора, Архимеда, Аристотеля и других ученых и инженеров. Человечество не скупилось на дифирамбы математике. В истории нашей цивилизации математика высоко ценилась не только за свои эффектные достижения в строительстве, астрономии, военном деле и других областях, но наряду с логикой она почиталась как гимнастика ума и даже возводилась в ранг «царицы наук». По мере развития математики и расширения прикладных возможностей рос и ее авторитет как науки. Так, Леонардо да Винчи утверждал, что бесспорная достоверность умозаключений в любой науке может достигаться только при использовании математических методов. Философ Р.Бэкон почти 800 лет назад выразился на этот счет куда более жестко и попросту обвинил в невежестве тех, кто не знает математику. Несмотря на излишнюю резкость, это высказывание, тем не менее, содержит изрядную долю истины. Ведь математика по существу не просто свод формул и приемов вычислений, а образец строгого логического и рационального мышления, направленного на решение совершенно конкретных задач познания окружающего мира и нашего жизнеустройства. Это подтверждают озвученные весной 2008 года результаты многолетних исследований ряда уважаемых зарубежных организаций, которые выявили тот факт, что ВВП на душу населения выше в странах с более высоким уровнем математической культуры граждан. Теперь понятно, что Дж. Буш уже располагал такой информацией, когда будучи президентом, призывал повысить уровень математической подготовки учащихся, хотя сам учился весьма посредственно.

В конце концов, почему знание искусства, в отличие от математики, всегда засчитывается в плюс? А ведь математика тоже искусство, причем высокое искусство интеллекта, весьма специфического рода. Вне зависимости от сферы приложения, эта наука по большому счету занимается научным обоснованием и формированием набора аналитических правил для логического заключения вида "если - тогда" и последующими числовыми расчетами на основе имеющихся исходных данных.

Математика уже давно и весьма успешно начала свое проникновение в область гуманитарных наук с немалой для них пользой. Она прочно заняла свое почетное место в управлении и бизнесе, принося прямую и немалую экономическую выгоду. В наше время убежденность в правильности принимаемого управленческого решения невозможно представить без соответствующего математического обоснования. Выпускник университета просто обязан иметь необходимую математическую подготовку.

В основе математики лежат определения и аксиомы, подсказанные интуицией, опытом и здравым смыслом. Эти базовые элементы с помощью логических рассуждений и математических построений преобразуются в целый арсенал математических методов. Созданное на таком, казалось бы зыбком, фундаменте всего лишь правдоподобных предположений и логических умозаключений здание математики, тем не менее, является грандиозным и весьма замысловатым по своей архитектуре, оставаясь в то же время стройным и изящным. Математика блестяще выдержала проверку временем. Изучая ее, испытываешь глубочайшее преклонение перед гением основоположников этой науки и их знаменитых последователей.

В настоящее время, несмотря на обилие учебной математической литературы, трудно найти один источник с рациональным сочетанием преподавания данного предмета на уровне Госстандарта и достаточного разнообразия жизненных примеров, которые убедительно показывают практическую значимость математики для широкой аудитории. В этом плане исключение составляют превосходные учебники МЭСИ (Московский государственный университет экономики, статистики и информатики). Однако они предназначены для подготовки специалистов экономико-математического и технического профиля и потому в полной мере не могут быть рекомендованы студентам МГУКИ.

В данном учебном пособии предпринята попытка компактного изложения разделов высшей математики в соответствии с требованиями ГОС к обязательному минимуму содержания основной образовательной программы при ограничении срока обучения этому предмету всего лишь одним семестром. В таких условиях обеспечить полное соответствие читаемого курса Госстандарту принципиально невозможно. Тем не менее, приводимые в пособии примеры практического применения математических методов призваны способствовать пониманию прикладных возможностей математики и развитию аналитического мышления с таким расчетом, чтобы с помощью приобретенных навыков будущий специалист эффективнее решал свои профессиональные задачи. Для достижения этой цели автор в меру возможности старался сделать читателей активными участниками математических построений.

В соответствии с требованиями АПИМ предлагаемое пособие в состоит из двух частей. Первая часть под названием “Элементы теории множеств” знакомит студентов с азами базового раздела математики, широко применяемого во многих разделах математики и, в том числе, в теории вероятностей. Здесь изучается своеобразный математический объект - множество. Во второй части “Теория вероятностей” представлена разделом “Случайные события”. Здесь находят свое научное объяснение выражения типа “пятьдесят на пятьдесят” или “девять против одного” и решаются более сложное задачи случайного мира, в котором мы по сути дела все и живем.

Добросовестное изучение материала пособия помимо общекультурного развития неизбежно даст ценный интеллектуальный опыт освоения в малознакомой сфере деятельности, весьма полезный в нашей изменчивой жизни.

Детализация изложения содержания курса совокупно с демонстрационными примерами, вопросами для самопроверки, задачами для самостоятельного решения, тестами и контрольными примерами позволяет адресовать это пособие не только студентам дневного обучения, но и студентам вечерней и заочной форм обучения в качестве методического материала.

Словарь символьных обозначений

Аналогично стенограммам для придания математическим записям компактного вида далее будут использована стандартная символика, читаемая в зависимости от контекста соответствующим образом:

⇒ - означает, что из левой части утверждения логически следует его правая

часть и читается как "следовательно", "вытекает";

⇔ - подразумевает, что из левой части утверждения логически следует его

правая часть, и наоборот; в зависимости от контекста читается как

"тогда и только тогда, когда", "необходимо и достаточно", "означает";

∊ - символ принадлежности; записи a∊M или M⋼a читаются так:

элемент а принадлежит множеству М или М содержит а;

Ï - не принадлежит;

Ì - принадлежит, содержит, включает для множеств (множество

A принадлежит множеству B или множество В включает А:

АÌВ);

Í - принадлежит или совпадает, т.е. допускается равенство

(совпадение) множеств;

= - множества равны, т.е. состоят из одинаковых элементов;

¹- множества не равны, т.е. отличаются по край ней мере одним

элементом.

: - раскрывает содержание предшествующей ему записи и читается

как “обладающий свойством” или ”такой, что”; используется в

описании множества в качестве разделителя его элемента и усло-

вия, которому он подчиняется.

$ - существует, найдется (квантор существования);

" - для всех, для любого (квантор всеобщности, произвольности).

Ч А С Т Ь 1

Э Л Е М Е Н Т Ы Т Е О Р И И М Н О Ж Е С Т В

Предыстория

С числами и действиями над ними знакомство происходит еще в школе. Числа в зависимости от своих свойств образуют множества натуральных, целых, рациональных и вещественных чисел.

Интуитивно ясно, что по смысловому содержанию множество представляет собой некоторую совокупность неких объектов. На этот счет люди задумывались уже в давние времена. Для демонстрации определенной условности самого понятия множества Евбулид, представитель логической школы эллинов предложил следующую апорию (вымышленная логически верная конструкция). На стол кладется одно зерно и задается вопрос - это куча зерна? Ответ естественно отрицательный. Затем кладется второе, третье, другие зерна и вопрос каждый раз повторяется вновь. Рано или поздно ответ окажется утвердительным, т.е. на столе по нашему представлению будет находиться куча зерна, отождествляемая с множеством. Затем, начинается обратная процедура изъятия из кучи одного зерна с последующим вопросом - оставшиеся зерна образуют кучу или нет. Эта процедура может повторяться до тех пор, пока на столе не останется последнее зерно или, дойдя до логического конца, не будет уже ни одного зерна. Таким образом, переход от качественного понятия “несколько” к “множество” и обратно осуществляется одним единственным зерном, что свидетельствует об отсутствии критерия, позволяющего четко разделять эти два понятия.

Элегантный выход из создавшегося положения нашел великий немецкий математик Георг Кантор (1845-1919 гг.), предложив философское определение множества, которое по своей сути звучит так. Множество М - совокупность различимых между собой объектов нашей интуиции и интеллекта, мыслимая как единое целое. Эти объекты называются элементами множества М.В данном контексте разница между “несколько” и “множество” нивелируется вплоть до совокупности, не содержащей ни одного элемента, называемой пустым множеством.

Понятие множества является одним из основополагающих в математике. Оно отражает наше понимание существования конечных и бесконечных совокупностей не только в природе (яблоки на дереве или звезды во вселенной), но и в нашем сознании (например, бесконечная последовательность чисел 1,2,3,… ).

В целостном виде теорию множеств Кантор представил миру в ХIХ веке. Он показал, что, как конечные, так и бесконечные множества можно сравнивать, оценивать их мощность, а также возможно производить над множествами ряд специфических математических операций. Теоретико-множественные идеи нашли себе широчайшее применение в различных разделах математики: числовые множества в математическом анализе, множества точек в геометрии, множества случайных событий в теории вероятностей, множества высказываний в математической логике.

В дальнейшем множества будут идентифицироваться прописными, а их элементы - строчными буквами. Например, запись 𝑎ÎА означает, что объект 𝑎 является элементом множества А, а СÌВ выражает факт принадлежности множества С множеству В, вследствие чего множество С называется подмножеством В.

Множество не содержащее ни одного элемента называется пустым и обозначается Æ.Очевидно, что "ВÊÆ (у любого множества имеется пустое подмножество).

Пример 1. Фраза “для любого числа 𝑎 множества А найдется такой число 𝑏 множества В, большее 𝑎, вследствие чего множество С является подмножеством В и не имеет общих элементов с А” записывается так: " 𝑎ÎА $𝑏ÎВ : 𝑎<𝑏 ⇒ СÍВ и С∩А=Æ.

Пример 2. Если - множество натуральных четных чисел, а - множество натуральных чисел кратных 3, то общие элементы этих множеств кратны 6, т.е. делятся на 6 нацело:

={𝑛ÎN: 𝑛/2ÎN}, ={𝑛ÎN: 𝑛/3ÎN} ⇒ ∩ ={𝑛ÎN: 𝑛/6ÎN}.

Очевидно ÌN и ÌN, где N - множество натуральных чисел.

M( , )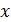

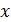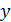r=1

Пример 3. Окружность единичного радиуса с центром в начале координат описывается с помощью теоремы Пифагора как геометрическое место точек плоскости, равноудаленных от центра:

L= .

Основные понятия и способы задания множеств

Множества будут обозначаться прописными, а их элементы строчными буквами. Принадлежность элемента 𝑚 множеству M записывается так: 𝑚ÎM; а множества A множеству B: АÍВ или АÌВ

и при этом говорят, что множество А является подмножеством множества В.Использованный здесь знак строго включения “Ì” означает, что "𝑎ÎA ⇒ 𝑎ÎB, но $ 𝑏ÎB : 𝑏ÏA, т.е. все элементы множества А являются одновременно элементами В, но при этом найдется такой элемент b множества B, который множеству А не принадлежит.

Важным свойством включения является транзитивность:

A Í В и В Í С ⇒ A Í С;

⇒ А Ì С.

Пример: A - связка спелых бананов; B - множество всех бананов;

C - множество всех фруктов; D - множество всех продуктов питания. Тогда очевидно имеет место строгое включение AÌBÌCÌD, т.е. каждое предыдущее множество является подмножеством последующего множества.

Очевидно, что каждый элемент множества является его подмножеством: 𝑎ÎA ⇒ {𝑎} Í A.

Далее, "АÍА (каждое множество является подмножеством самого себя). В последствие в процессе качественных рассуждений в случае A Í В будет использовано выражение В “больше” А или А “меньше” В.

Множества А и В называются равными, если они состоят из одних и тех же элементов, т.е. элементы одного множества являются одновременно элементами другого множества или, что то же самое, каждое из этих множеств является подмножеством другого.

Иными словами равенство множеств означает совпадение их всех элементов в соответствии с принципом сравнения объектов путем их реального или мысленного наложения (сопоставления), который использует наш интеллект для этой цели.

В символьной записи это определение выглядит так:

А=В ⇔

Рассуждая от противного нетрудно убедиться, что А¹В ⇔ $ 𝑎ÎA : 𝑎ÏB или $ bÎB : bÏA, а может и то и другое, т.е. в по крайней мере в одном из множеств найдется элемент, который другому множеству не принадлежит.