Метод узловых потенциалов

Исходные данные

R₁ = 11 Ом; R₄ = 37 Ом; R₇ = 24 Ом; E₁ = 10 В;

R₂ = 21 Ом; R₅ = 18 Ом; R₈ = 37 Ом; Е₂ = 21 В;

R₃ = 46 Ом; R₆ = 28 Ом; R₀ = 0,1 Ом; Е₃ = 46 В;

J₁ = 0,3 А;

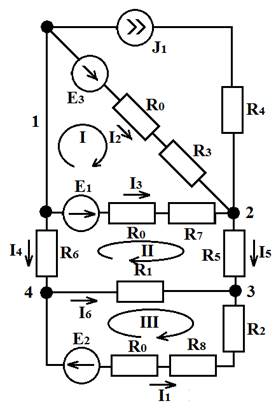
Определить значение токов протекающих в каждой ветви рассматриваемой цепи.

Метод законов Кирхгофа

Рассматриваемая схема содержит 7 ветвей. В одной ветви ток считается известным и равным току источника тока (J₁). Неизвестных токов 6. Для их определения составляем систему уравнений 6-ого порядка. По первому закону Кирхгофа необходимо составить n-1 уравнений (где n – количество узлов). Остальные уравнения составляются по второму закону Кирхгофа.

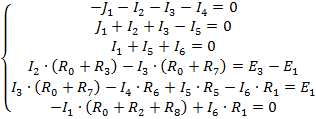
Данную систему приводим в удобный вид, выполнив над ней некоторые математические преобразования:

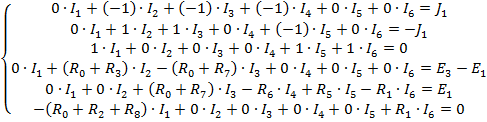
Полученную систему уравнений записываем в матричном виде:

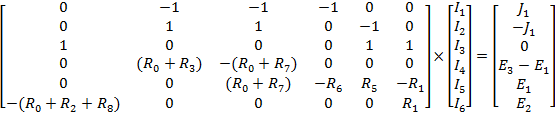
Полученную систему уравнений решаем относительно токов одним из известных методов решения систем алгебраических уравнений (Методом Крамера):

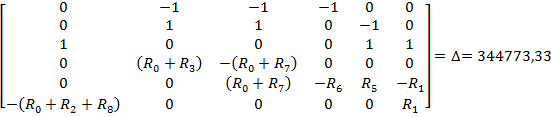
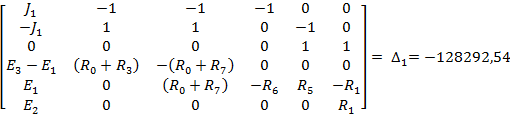
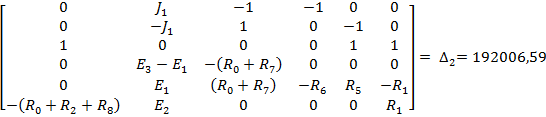
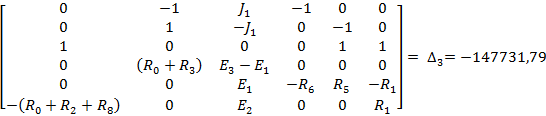
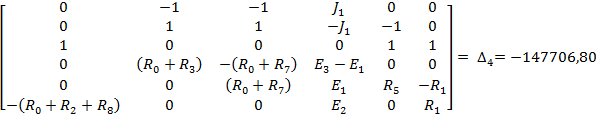
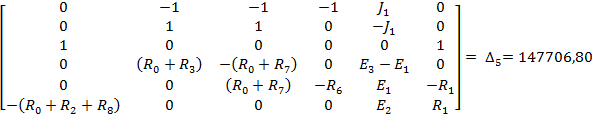
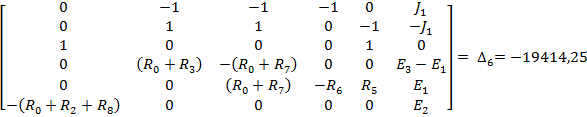
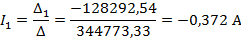
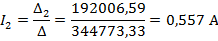
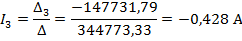
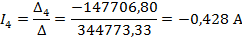
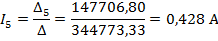
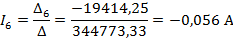
Для проверки полученного решения с помощью баланса мощностей, необходимо найти напряжение на ветви с источником тока:

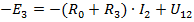, от сюда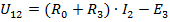

Полученные решения проверяем с помощью баланса мощностей:

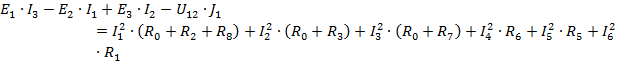
35,245 Вт = 35,245 Вт

Метод контурных токов

Сформируем систему уравнений, используя следующие правила:

1. R₁₁, R₂₂, R₃₃ …. – элементы, стоящие на главной диагонали матрицы при неизвестных. Данные коэффициенты являются контурными сопротивлениями и формируются, как сумма сопротивлений входящих в контур.

2. Для всех остальных коэффициентов матрицы сопротивлений – их значения определяются суммой сопротивлений ветвей, в которых протекают контурные токи, принадлежащие двум соседним контурам. При этом значение элементов берется со знаком минус, если контурные токи в данной ветви встречаются, в противном случае значение элемента берется со знаком плюс.

3. Е₁₁, Е₂₂, Е₃₃ …. – контурные ЭДС. Определяются, как алгебраическая сумма ЭДС, действующих в контуре.

Контурный ток – ток, протекающий в контуре.

R₁₁ = R₀ + R₃ + R₀ + R₇ Е₁₁ = Е₃ – Е₁ + J₁ · (R₀ + R₃)

R₂₂ = R₀ + R₇ + R₁ + R₅ + R₆ Е₂₂ = Е₁

R₃₃ = R₁ + R₂ + R₀ + R₈ Е₃₃ = Е₂

R₁₂ = R₂₁ = -(R₀ + R₇)

R₁₃ = R₃₁ = 0

R₂₃ = R₃₂ = -R₁

Запишем данные уравнения в матричном виде:

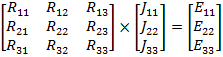
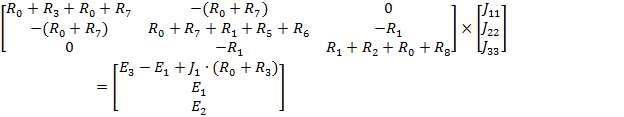
Полученную систему уравнений решаем относительно контурных токов одним из известных методов решения систем алгебраических уравнений (Методом Крамера):

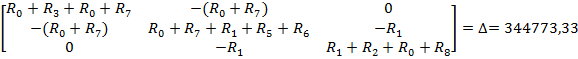
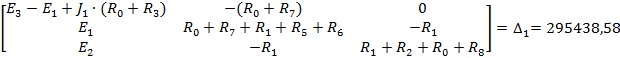
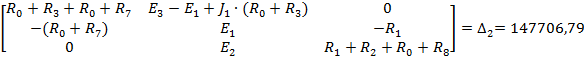
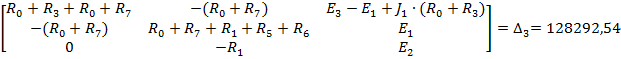
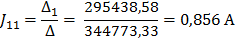
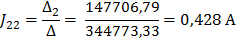
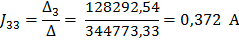
По найденным значениям контурных токов определяем токи в ветвях:

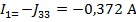
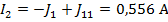
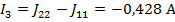
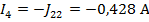
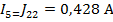
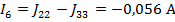
Полученные решения проверяем с помощью баланса мощностей:

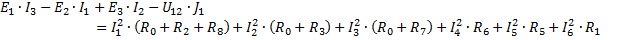
35,245 Вт = 35,245 Вт

Метод узловых потенциалов

Сформируем систему уравнений, используя следующие правила:

1. 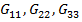- сумма проводимости ветвей входящих в рассматриваемый узел.

2. Остальные элементы матрицы проводимости представляют собой сумму проводимости ветвей соединяющих i и j узлы, при этом данные коэффициенты всегда берутся со знаком минуса.

3. 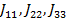– матрица узловых токов. Формируется согласно направлению источников тока и ЭДС относительно рассматриваемого узла. Если источник тока или ЭДС направлен к узлу, его значение берется со знаком плюс, в противном случае - со знаком минус.

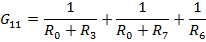
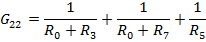
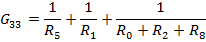
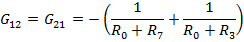
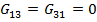
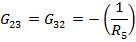
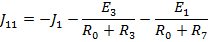
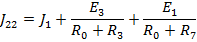
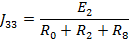
Запишем данные уравнения в матричном виде:

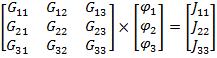
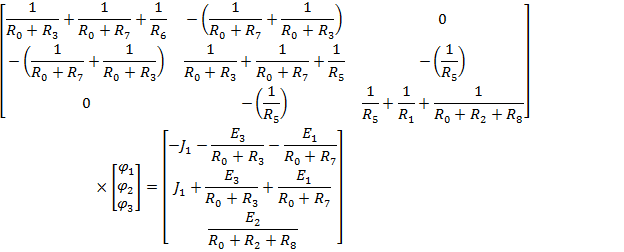
Полученную систему уравнений решаем относительно узловых потенциалов одним из известных методов решения систем алгебраических уравнений (Методом Крамера):

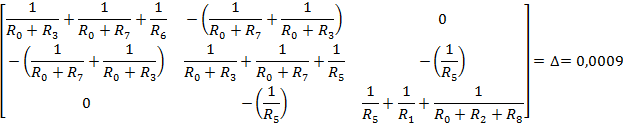
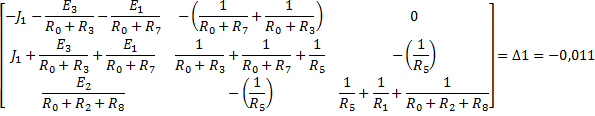
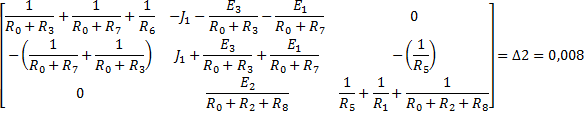
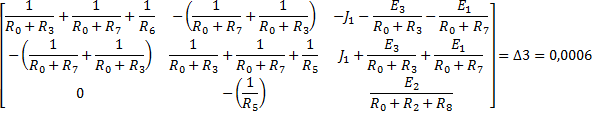
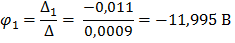
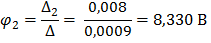
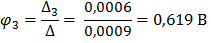
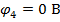
По найденным значениям узловых потенциалов находим токи в ветвях:

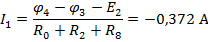
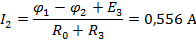
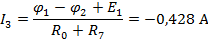
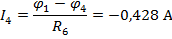
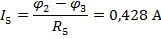
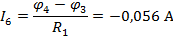
Полученные решения проверяем с помощью баланса мощностей:

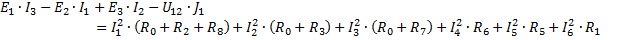
35,245 Вт = 35,245 Вт