Структурная оптимизация распределенных систем обслуживания

В общем случае под распределенными системами обслуживания понимают совокупность следующих элементов:

- закрепленная территория или зона ответственности;

- множество распределенных обслуживающих объектов {S};

- система сбора информации и заявок от обслуживаемых объектов{Q};

- система управления.

Система моделирования РСО должна обеспечивать выполнение следующих функций : Отображение окружающей среды. На каждом шаге моделирования необходимо задать характеристики каждого элемента пространства A(I,J)=(P1, … Pk). Вычислительная сложность операции определяется только размерностью пространства моделирования N2 и числом параметров k. Отображение объектов обслуживания. Этот этап требует задания параметров элементов {Q}. Сложность операции линейно зависит от количества объектов - источников заявок М и степени детализации их описания Q(I)=(X,Y,P1, … Pr), где X и Y координаты объекта, а Pi его свойства.Отображение обслуживающих объектов. Этот этап требует задания параметров элементов {S}. Сложность операции линейно зависит от количества обслуживающих объектов K и степени детализации их описания S(I)=(X,Y,P1, … Pr), где X и Y координаты объекта, а Pi его свойства. Параллельная реализация этой операции не эффективна. Оценки эффективности системы управления. Результатом моделирования РСО должна стать оценка того, справится ли система с нагрузкой, заданной {Q} в состоянии, заданном {A} и {S}, и если нет, Визуализация результатов моделирования. Вычислительная сложность процесса визуализации зависит от представляемой информации и в общем виде достаточно трудна для оценки. Представленные соображения позволяют предложить следующую структуру системы моделирования РСО:- последовательная подсистема моделирования обслуживающих объектов и заявок, внешней среды;- параллельная подсистема оценки эффективности системы обслуживания; - унифицированная подсистема визуализации результатов моделирования. Такой подход приведет к сокращению сроков разработки и снижению затрат на создание новых систем моделирования РСО. Теоретическая оценка математического ожидания числа бросков F (операций rand), необходимых для заполнения вектора уникальными числами дает следующий результат: При выполнении расчетов вычислительная нагрузка равномерно распределялась между узлами системы, а результат получался редуцированием на ведущем узле. Проведенные эксперименты подтверждают практическую возможность использования многопроцессорных вычислительных систем для выполнения этапа оценки состояния распределенной системы обслуживания.

Функция полезности

Пусть заданы критерии K1,…,Kn; X = { x | x = (x1,…,xn) } – множество векторных оценок вариантов по этим критериям. Пусть на X задано R – отношение предпочтения. Числовая функция f : X → R , называется функцией полезности, если она обладает следующим свойством: f(x) ≥ f(y) ⇔ x R y.

Если известна функция полезности, то поиск оптимального варианта сводится к задаче нахождения x* = arg max f(x), x∈X – аргумента максимума функции полезности на множестве X.

Методы построения функции полезности делятся на эвристические и аксиоматические.

К эвристическим методам можно отнести метод главного критерия и метод обобщенного критерия. Метод главного критерия сводится к оптимизации по одному выбранному критерию, при условии, что остальные критерии не больше (или не меньше) приемлемых значений. Метод обобщенного критерия заключается в свёртке набора критериев в числовую функцию, которая и будет являться функцией полезности.

Виды свёрток:

1) аддитивная свёртка: f = α1K1+…+αnKn;

2) мультипликативная свёртка: f = exp(α1ln(K1)+…+αnln(Kn)) = = *…*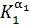

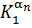
3) приведенная свёртка: f = min(Ki/αi) по всем i=1…n (или f = max(Ki/αi) по

всем i=1…n).

Аксиоматические методы построения функции полезности – это формальные методы, основанные на том, что формулируются специальные предположения (аксиомы) о свойствах предпочтения, выполнение которых гарантирует существование функции полезности конкретного вида. Обычно, при использовании таких методов функцию полезности строят в аддитивном виде: f = λ1f1+…+λnfn как сумму функций полезности по каждому критерию с некоторыми весовыми коэффициентами λ1,…,λn.

Методы компромиссов

X-вектор решений

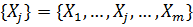– сов-сть показателей

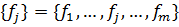– част. Показ.

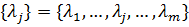– веса частн. Показ.

Принципы(группы):

1. Принцип равномерности

1.1. Принцип равенства – Альт., у которой все показатели имеют одинаковое отклонение от оптим., лучшая.

1.2. Принцип квазиравенства – Та альт. лучше, у которой пронорм. безразмерн. показ. равны между собой с учетом допуска.

1.3. Принцип максимина – Та альт. лучше, у кот. миним. знач. безразм. показат. больше.

2. Принцип справедливой уступки

2.1. Принцип абсолютной уступки – Лучше та альт., у кот. сумма приращений матор. ≥суммы минир. показат.

2.2. Принцип относит. уступки - Наилучшей считается такая альт., при которой суммарный относительный уровень снижения одного или нескольких критериев не превосходит относительного суммарного уровня повышения по остальным критериям.

2.3. Принцип выделения 1 оптимизир. показат. – Выбир. та альт., у кот. главный показатель имеет оптим. значение, а остальные в пределах нормы.