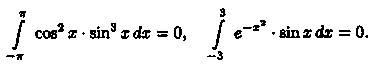Формула Ньютона-Лейбница. Простым и удобным методом вычисления определенного интеграла от непрерывной функции
Простым и удобным методом вычисления определенного интеграла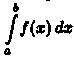 
от непрерывной функции является формула Ньютона-Лейбница:
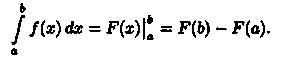
Применяется этот метод во всех случаях, когда может быть найдена первообразная функции F(x) для подынтегральной функции ƒ (х).
Например,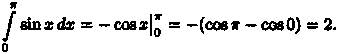 
При вычисленииопределенных интегралов широко используется метод замены переменной и метод интегрирования по частям.
Интегрирование подстановкой (заменой переменной)
Пусть для вычисления интеграла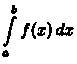 
от непрерывной функции
сделана подстановка х = φ(t).
Теорема 39.1. Если:
1) функция х = φ(t) и ее производная х' = φ'(t) непрерывны при t є [а;β];
2) множеством значений функции х = φ(t) при t є [а,β] является отрезок [а; b];
3) φ(а)=а и φ(β)=b.
то
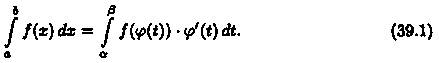
▼Пусть F(x) есть первообразная для ƒ(х) на отрезке [а;b]. Тогда по формуле Ньютона-Лейбница 
Так как (F(φ(t))' = f(φ(t)) - φ'(t),то F(φ(t)) является первообразной для функции f(φ(t)) -φ'(t), t Î [а;β]. Поэтому по формуле Ньютона—Лейбница имеем
▲
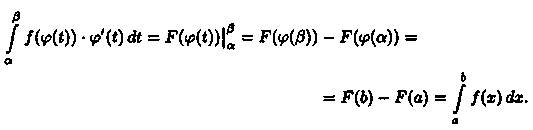Формула (39.1) называется формулой замены переменной в определенном интеграле. Отметим, что:
1) при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется;
2) часто вместо подстановки х = φ(t) применяют подстановку t = g(x);
3) не следует забывать менять пределы интегрирования при замене переменных!
Пример 39.1. Вычислить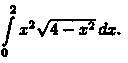 
Решение: Положим х = 2 sin t, тогда dx = 2 cos t dt. Если х=0, то t = 0; если x = 2, то t =. Поэтому
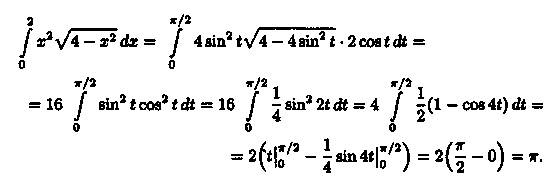
Интегрирование по частям
Теорема 39.2. Если функции u = u(х) и v = v(x) имеют непрерывные производные на отрезке [а; b], то имеет место формула
▼На отрезке [а; b] имеет место равенство (uv)' = u'v+uv'. Следовательно, функция uv есть первообразная для непрерывной функции u'v+uv'. Тогда по формуле Ньютона-Лейбница имеем:
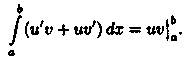
Следовательно,
▲
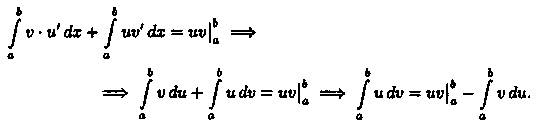Формула (39.2) называется формулой интегрирования по частям для определенного интеграла.
Пример 39.2. Вычислить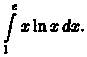 
Решение: Положим
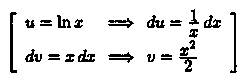
Применяя формулу (39.2), получаем
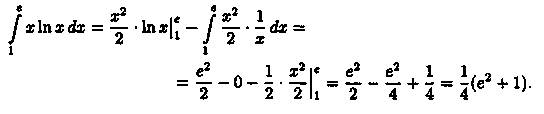
Пример 39.3. Вычислить интеграл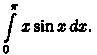 
Решение: Интегрируем по частям. Положим
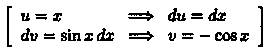
Поэтому
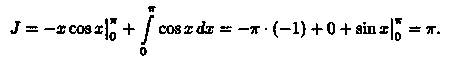
Интегрирование четных и нечетных функций в симметричных пределах
Пусть функция ƒ(х) непрерывна на отрезке [-а; а], симметричном относительно точки х = 0. Докажем, что
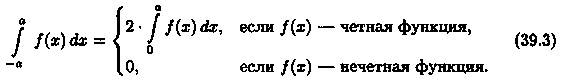
▼Разобьем отрезок интегрирования [-а; а] на части [-а; 0] и [0; а]. Тогда по свойству аддитивности
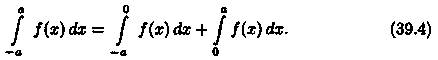
В первом интеграле сделаем подстановку х = -t. Тогда
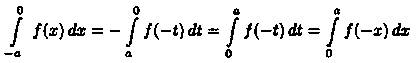
(согласно свойству: «определенный интеграл не зависит от обозначения переменной интегрирования»). Возвращаясь к равенству (39.4), получим
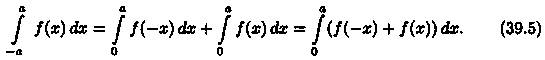
Если функция ƒ(х) четная (ƒ(-х) = ƒ(х)), то ƒ(-х) + ƒ(х) = 2ƒ(х); если функция ƒ(х) нечетная (ƒ(-х) = - ƒ(х)), то ƒ(-х) + ƒ(х) = 0. Следовательно, равенство (39.5) принимает вид (39.3).▲
Благодаря доказанной формуле можно, например, сразу, не производя вычислений, сказать, что
