Расчет и исследование двухконтурной астатической САР

Задание на курсовую работу.

Исследование внутреннего контура регулирования САР.

2.1 Составление схемы оптимальной двухконтурной САР стр.

2.2 Определение передаточной функции регулятора внутреннего контура стр.

2.3 Передаточные функции внутреннего оптимального разомкнутого контуров регулирования стр.

2.4 Аналитический расчет графиков переходных процессов оптимального внутреннего замкнутого контура САР стр.

2.5 Исследование динамических свойств внутреннего контура регулирования САР при изменении параметров регулирования стр.

2.6 Исследование динамических свойств внутреннего контура регулирования САР при изменении постоянной времени обратной связи регулятора T_р1 стр.

3. Расчет и исследование двухконтурной статической САР с последовательной коррекцией.

3.1 Составление структурной схемы двухконтурной САР стр.

3.2 Передаточные функции замкнутой и разомкнутой САР, по управляющему и возмущающему воздействиям стр.

3.3 Передаточные функции внешнего контура для управляющего воздействия стр.

3.4 Аналитический расчет переходных процессов стр.

3.5 Экспериментальное определение кривых переходных процессов с помощью программы MathLab стр.

3.6 Расчет и построение асимптотических ЛАЧХ и ЛФЧХ разомкнутых САР стр.

3.7 Выводы стр.

Расчет и исследование двухконтурной астатической САР.

4.1 Структурная схема САР, настроенной по симметричному оптимуму стр.

4.2 Расчет и построение ЛАЧХ и ЛФЧХ разомкнутой САР стр.

4.3 Произвести аналитический расчет переходных процессов САР стр.

4.4 Экспериментальный расчет переходных процессов стр.

1. Задание на курсовую работу

Для заданного объекта регулирования (рис. 1) произвести построение и расчет двухконтурной схемы САР (статической и астатической), выбрать и рассчитать регуляторы в контурах регулирования, выполнить построение логарифмических частотных характеристик, а также кривых переходных процессов при управляющем и возмущающем воздействиях, определить качество регулирования САР.

Рисунок 1.

Параметры объекта регулирования:

- постоянная времени фильтра;

=0,01

- коэффициент усиления фильтра;

Кф=12

- коэффициент усиления апериодического звена;

К0=10

и - постоянные времени элементов объекта регулирования;

=

Т01=0,04

Т02=0,12

2.Исследование внутреннего контура регулирования САР

2.1 Составление схемы оптимальной двухконтурной САР

Оптимальная схема САР составляется на основании принципа построения систем подчиненного регулирования. Согласно этому принципу число контуров регулирования, т.е число регуляторов принимается равным числу больших постоянных времени. В нашем случае система должна содержать два контура регулирования с двумя регуляторами, один из которых компенсирует первую постоянную времени, а второй – вторую постоянную времени. Построение структурной схемы регулирования обычно начинают с внутреннего контура, в который входит звено с малой постоянной времени и одной большой постоянной времени. Перед объектом регулирования ставят регулятор W_рег1(p) и охватываем единичной обратной связью. Затем строиться второй контур регулирования с второй большой постоянной времени. На вход ставят второй регулятор W_рег2(p) (См. рис.2) .

P

Рисунок 2- Структурная схема оптимальной двухконтурной САР

2.2 Определение передаточной функции регулятора внутреннего контура

Обобщенная формула:

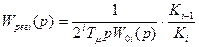
где i =1– номер рассматриваемого контура;

T_μ =0,015 – наименьшая некомпенсируемая постоянная времени;

T_μ =0,01

W_0i(p) – передаточная функция той части объекта регулирования, которая должна быть скомпенсирована регулятором рассматриваемого контура.

K_i - коэффициенты обратной связи внутреннего контура;

K_i-1 – коэффициенты обратной связи предыдущего контура.

Передаточная функция объекта регулирования имеет вид:

Передаточная функция регулятора примет вид:

Для того чтобы система была оптимальной необходимо принять:

T_p1=T₀₁=0,075с, а T_p=2T_μK_фK₀=2·0,015·8·6=1,44 с.

T_p1=T₀₁=0,04с, а T_p=2T_μK_фK₀=2·0,01·12·10=2,4 с.

2.3 Передаточные функции внутреннего оптимального разомкнутого контуров регулирования

Передаточная функция оптимального разомкнутого контура имеет вид:

Передаточная функция оптимального замкнутого контура имеет вид:

2.4 Аналитический расчет графиков переходных процессов оптимального внутреннего замкнутого контура САР

Для получения выражения переходной функции h(t) применим обратное преобразование Лапласа. После нахождения корней, полученной функции h(t) получим следующее выражение для переходной функции

Основные показатели представленного на рисунке 2.1

1) Перерегулирование :

s % = ,

где: y_max – максимальный выброс регулируемой координаты;

y_уст – установившееся значение регулируемой координаты.

2) Время регулирования 0,16

3) Время установления 1

4) Время максимального перерегулирования 1,043

Рисунок 2.1 - Кривая переходного процесса h(t) замкнутой САР

2.5 Исследование динамических свойств внутреннего контура регулирования САР при изменении параметров регулирования

2.5.1 Исследуем три варианта изменения постоянной времени интегрирования регулятора:

при c

2.5.1.1 Передаточные функции разомкнутой и замкнутой САР

Для первого случая:

; Т_р1 = Т₀₁ = 0,075– оптимальная настройка.

Передаточная функция оптимального разомкнутого контура имеет вид:

Передаточная функция оптимального замкнутого контура имеет вид:

Где: c, а

Для второго случая:

<

Передаточная функция разомкнутого контура имеет вид:

Передаточная функция замкнутого контура имеет вид:

Для третьего случая:

>

Передаточная функция разомкнутого контура имеет вид:

Передаточная функция замкнутого контура имеет вид:

2.5.1.2 Расчет и построение логарифмических частотных характеристик замкнутого и разомкнутого внутреннего контура САР

Первый случай:

; Т_р1 = Т₀₁ = 0,075– оптимальная настройка.

Выражения для ЛАЧХ разомкнутого и замкнутого контура имеют вид:

где k=1

0.707

Подставляя данные получим:

Графики асимптотических ЛАЧХ представлены на рис 2.3 и рис 2.4

Выражение для ЛФЧХ разомкнутого и замкнутого контура САР имеют вид:

при

при

Подставляя данные получим:

2) <

Выражения для ЛАЧХ и ЛФЧХ разомкнутого контура САР имеют вид:

Где k=1

Подставляя данные получим:

Графики асимптотических ЛАЧХ представлены на рис. 2.3 и 2.4

Для ЛФЧХ разомкнутого контура САР выражения имеют такой же вид как и в предыдущем случае.

3) >

Выражения для ЛАЧХ разомкнутого и замкнутого контура САР имеют вид:

Где k=1

Подставляя, получим:

Как и в предыдущих случаях получаем следующие выражения для ЛФЧХ разомкнутого и замкнутого контура САР:

Рисунок 2.2 - Логарифмические частотные характеристики разомкнутой САР

Рисунок 2.3 - Логарифмические частотные характеристики замкнутой САР

а) Частоты срезы w_с:

- для разомкнутой САР: w_с1 = 16,5; w_с2 = 32; w_с3 = 52,5;

- для замкнутой САР: w_с1 = 4; w_с2 =20; w_с3 = 60.

На рисунке 2.5 –ЛАЧХ и ЛФЧХ разомкнутого контура при изменении Т_р

На рисунке 2.6 - ЛАЧХ и ЛФЧХ замкнутого контура при изменении Т_р

б) Запас устойчивости по фазе m = 180 - j(w_с):

- для разомкнутой САР:

m₁ = 180 - j(w_с1) = 180 - j(16,5) = 180 – 103 = 77;

m₂ = 180 - j(w_с2) = 180 - j(32) = 180 – 115 = 65;

m₃ = 180 - j(w_с3) = 180 - j(52,5) = 180 – 127 = 53;

- для замкнутой САР:

m₁ = 180 - j(w_с1) = 180 - j(4) = 180 – 17 = 163;

m₂ = 180 - j(w_с2) = 180 - j(20) = 180 – 36 = 144;

m₃ = 180 - j(w_с3) = 180 - j(60) = 180 – 78 =102.

2.5.1.3 Расчет переходных процессов по методу моделирования на компьютере

С помощью программы автоматического моделирования MATLAB произведем моделирование. Для этого используем файл MATLAB-SIMULINK

Исследование проводилось для трех случаев:

при c

Кривые, полученные при помощи программы MATLAB, представлены на рисунке 2.4

Рисунок 2.4 - Исследование динамических свойств внутреннего контура

1) Относительное время регулирования :

2) Перерегулирование

2.6. Исследование динамических свойств внутреннего контура регулирования при изменении постоянной времени обратной связи регулятора T_р1

2.6.1.Исследуем САР для трех случаев: