Первая задача анализа на чувствительность (анализ на чувствительность к правой части ограничений)

Проанализируем чувствительность оптимального решения задачи №1.01 о производстве красок. ОДР задачи №1.01 (рис.3.1) – многоугольник ABCDEF. В оптимальной точке Е пересекаются прямые (1) и (2). Поэтому ограничения (1) и (2) являются связывающими, а соответствующие им ресурсы (ингредиенты А и В) – дефицитными.

Рассмотрим экономический смысл этих понятий. Точка максимума ЦФ Е соответствует суточному производству 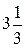т краски 1-го вида и 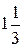т краски 2-го вида. В производстве красок используются ингредиенты А и В. Суточный запас на складе ингредиентов А и В – это правые части связывающих ограничений (1) и (2) (6 и 8 т ингр./сутки). Согласно этим ограничениям, на производство в точке Е расходуется

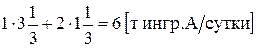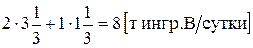(1) и (2).

Рис.3.1. Графическое решение задачи №1.01 о красках

Таким образом, понятие "связывающие ограничения" (1) и (2) означает, что при производстве красок в точке 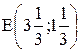запасы ингредиентов А и В расходуются полностью и по этой причине невозможно дальнейшее наращивание производства. В этом заключается экономический смысл понятия дефицитности ресурсов, т.е. если фирма сможет увеличить суточные запасы ингредиентов, то это позволит увеличить выпуск красок. В связи с этим возникает вопрос: до какого уровня целесообразно увеличить запасы ингредиентов и на сколько при этом увеличится оптимальное производство красок?

Правило №3.1

Чтобы графически определить максимальное увеличение запаса дефицитного ресурса, вызывающее улучшение оптимального решения,

необходимо передвигать соответствующую прямую в направлении улучшения ЦФ до тех пор, пока это ограничение не станет избыточным.

При прохождении прямой (1) через точку К (рис.3.2) многоугольник ABCKF становится ОДР, а ограничение (1) – избыточным. Действительно, если удалить прямую (1), проходящую через точку К, то ОДР ABCKF не изменится. Точка К становится оптимальной, в этой точке ограничения (2) и (4) становятся связывающими.

Рис.3.2. Анализ увеличения ресурса А

Правило №3.2

Чтобы численно определить максимальную величину запаса дефицитного ресурса, вызывающую улучшение оптимального решения,

необходимо:1) определить координаты точки 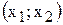, в которой соответствующее ограничение становится избыточным;

2) подставить координаты 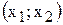в левую часть соответствующего ограничения.

Координаты точки К(3;2) находятся путем решения системы уравнений прямых (2) и (4). Т.е. в этой точке фирма будет производить 3 т краски 1-го вида и 2 т краски 2-го вида. Подставим 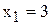и 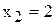в левую часть ограничения (1) и получим максимально допустимый запас ингредиента А

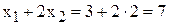[т ингр.А/сутки].

Дальнейшее увеличение запаса ингредиента А нецелесообразно, потому что это не изменит ОДР и не приведет к другому оптимальному решению (см. рис.3.2). Доход от продажи красок в объеме, соответствующем точке К, можно рассчитать, подставив ее координаты (3;2) в выражение ЦФ

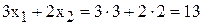[тыс.руб./сутки].

Рассмотрим вопрос о целесообразности увеличения запаса ингредиента В. Согласно правилу №3.1, соответствующее ограничение (2) становится избыточным в точке J, в которой пересекаются прямая (1) и ось переменной 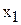(рис.3.3). Многоугольник ABCDJ становится ОДР, а точка J(6;0) – оптимальным решением.

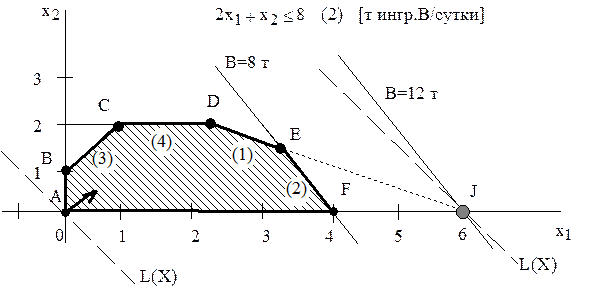
Рис.3.3. Анализ увеличения ресурса В

В точке J выгодно производить только краску 1-го вида (6 т в сутки). Доход от продажи при этом составит

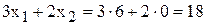[тыс.руб./сутки].

Чтобы обеспечить такой режим работы, согласно правилу №3.2, запас ингредиента В надо увеличить до величины

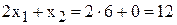[т ингр.В/сутки].

Ограничения (3) и (4) являются не связывающими, т.к. не проходят через оптимальную точку E (см. рис.3.1). Соответствующие им ресурсы (спрос на краски) являются недефицитными. С экономической точки зрения это означает, что в данный момент уровень спроса на краски непосредственно не определяет объемы производства. Поэтому некоторое его колебание может никак не повлиять на оптимальный режим производства в точке E.

Например, увеличение (уменьшение) спроса на краску 2-го вида будет соответствовать перемещению прямой ограничения 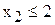(4) вверх (вниз). Перемещение прямой (4) вверх никак не может изменить точку Е максимума ЦФ. Перемещение же прямой (4) вниз не влияет на существующее оптимальное решение только до пересечения с точкой Е (см. правило №3.3). Из рис.3.1 видно, что дальнейшее перемещение (4) приведет к тому, что точка Е будет за пределами новой ОДР, выделенной более темным цветом. Кроме того, любое оптимальное решение для этой новой ОДР будет хуже точки Е.

Правило №3.3

Чтобы определить максимальное уменьшение запаса недефицитного ресурса, не меняющее оптимальное решение,

необходимо передвигать соответствующую прямую до пересечения с оптимальной точкой.

Правило №3.4

Чтобы численно определить минимальную величину запаса недефицитного ресурса, не меняющую оптимальное решение,

необходимо подставить координаты оптимальной точки в левую часть соответствующего ограничения.

Чтобы выяснить, до каких пределов падение спроса на краску 2-го вида не повлияет на производство в точке 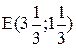, используем правило №3.4. Подставляем в левую часть ограничения (4) координаты точки Е, получаем

.

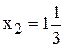Делаем вывод: предельный уровень, до которого может упасть спрос на краску 2-го вида и при котором не изменится оптимальность полученного ранее решения, равен 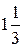т краски в сутки.

Экономический смысл ограничения (3)

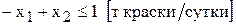
в том, что объем продаж краски 2-го вида может превысить объем продаж краски 1-го вида максимум на 1 т. Дальнейшее увеличение продаж краски 2-го вида по сравнению с краской 1-го вида графически отобразится перемещением прямой (3) влево и вверх, но никак не повлияет на оптимальность точки Е. Но если разность спросов на краску 2-го и 1-го видов будет уменьшаться, то прямая (3) будет перемещаться ниже и правее. Последним положением прямой (3), при котором точка Е остается оптимальной, является пересечение с точкой Е (см. рис.3.1). Согласно правилу №3.4, подставим координаты точки 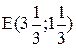в левую часть ограничения (3)

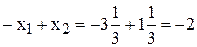[т краски].

Получаем, что разность спросов на краску 2-го и 1-го вида в точке стала отрицательной. То есть, прохождение прямой (3) через точку Е означает, что краску 2-го вида будут покупать в меньшем объеме, чем краску 1-го вида

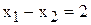[т краски/сутки].

Делаем вывод: максимальное превышение спроса на краску 1-го вида над спросом на краску 2-го вида, при котором оптимальное решение в точке Е не изменится, составляет 2 т краски в сутки.

Результаты решения первой задачи анализа оптимального решения на чувствительность представлены в табл.3.1.

Таблица 3.1