Округленное время жизни

Обычно люди ведут счет прожитых лет целыми годами, а страховые компании обычно заключают договоры страхования жизни на 1, 3, 5 и т.п. целое число лет. Поэтому естественно рассмотреть наряду с обычной продолжительностью жизни 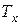ее целую часть 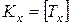. Таким образом, если, например, 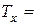18 лет 9 месяцев = 18.75 лет, то 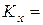18 лет. Величина 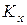называется округленной (урезанной) остаточной продолжительностью жизни. Следует подчеркнуть, что округление производится не до ближайшего целого, а всегда с недостатком (т.е. до ближайшего целого, меньшего, чем данное дробное число). В этом смысле английский термин curtate (“урезанная”) точнее, чем принятый нами термин “округленная”.

Распределение округленного времени жизни

Поскольку случайная величина 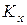принимает только целые значения, ее стохастическая природа характеризуется (как это принято в теории вероятностей) не функцией распределения, а распределением, т.е. набором вероятностей 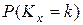, 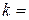0, 1, 2,…

Так как событие 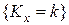эквивалентно тому, что 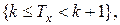верно равенство:

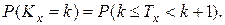
Вероятность 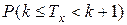в силу непрерывности случайной величины 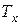равна вероятности 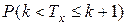, которая была обозначена как 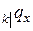. Выразим распределение случайной величины 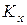в терминах функции выживания:

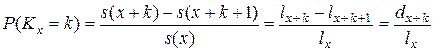
и в терминах интенсивности смертности:

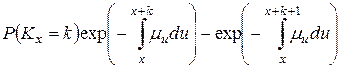
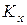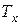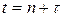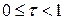Функция распределения округленного времени жизни достаточно просто связана с функцией распределения точного времени жизни . А именно, пусть , где (так что ).

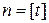Тогда

.

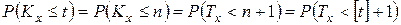Ранее было рассмотрено остаточное время жизни 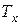и исходная случайная величина теории страхования – продолжительность жизни 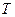. Однако поскольку 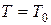, то, в частности, распределение округленного времени жизни 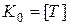может быть определено по формуле:

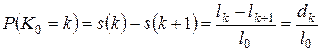
или

.

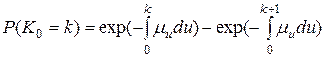Зависимость 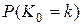от 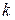приближенно может быть описана с помощью 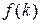, где 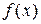– плотность распределения случайной величины 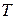. Таким образом, кривая смертей дает представление и о распределении округленного времени жизни.

Среднее округленное время жизни и его дисперсия

Математическое ожидание случайной величины 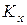называется средней округленной продолжительностью жизни и обозначается :

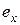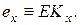
В соответствии с общей формулой для дискретной случайной величины

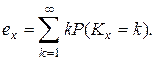
Тогда 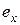в терминах функции выживания:

.

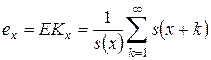Подобным же образом для второго момента 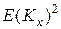, который необходим для расчета 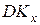, получим:

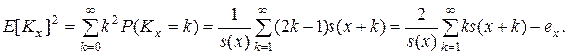
Более интересной является рекуррентная формула

,

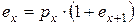откуда вытекает следующее соотношение, связывающее среднее округленное время жизни и вероятность смерти в течение ближайшего года:

.

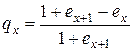Для доказательства этого соотношения прежде всего отметим, что

.

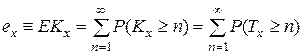Но

.

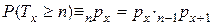Поэтому

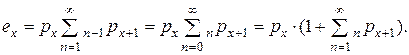
Сумм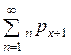а равна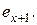

Итак,

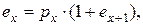
откуда:

,

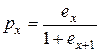что равносильно доказываемому соотношению.