Задачи для самостоятельного решения. Вариант 1(по списку: 1, 6, 11, 16)

Вариант 1(по списку: 1, 6, 11, 16). Написать программу с базовым классом для реализации ком­плексных чисел в алгебраической форме и основных операций с ними: сложения, вычитания, умножения и деления. Путем наследования создать производный класс, в котором определить операции вычисления модуля комплексного числа и комплексно спряженного.

Вариант 2(по списку: 2, 7, 12, 17). Написать программу с классом для реализации комплексного числа в тригонометрической форме и основных операций с ними: сложе­ния, вычитания, умножения и деления. Путем наследования создать произ­водный класс, в котором определить операции вычисления действительной и мнимой частей комплексного числа, а также комплексно спряженного.

Вариант 3(по списку: 3, 8, 13, 18). Написать программу с классом для реализации комплексных чисел в алгебраической форме и определить основные операции: сложение, вычитание, умножение и деление (в том числе и на действительные числа). Создать производный класс, в котором определить метод для вычисления комплексной экспоненты .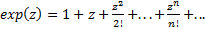

Вариант 4(по списку: 4, 9, 14, 19).Написать программу с классом для реализации комплексных чисел в алгебраической форме и определить основные операции: сложение, вычитание, умножение и деление. Создать производный класс, в котором определить метод для вычисления комплексного косинуса .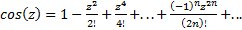

Вариант 5(по списку: 5, 10, 15, 20). Написать программу с классом для реализации комплексных чисел в алгебраической форме и определить основные операции: сложение, вычитание, умножение и деление (в том числе и на действительные числа). Создать производный класс, в котором определить метод для вычисления комплексного синуса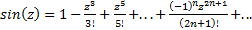

Практическая работа № 9

Тема: «Шаблоны»

Примеры решения задач

Здесь рассматриваются некоторые примеры создания программных кодов, в которых используются шаблоны.

Обобщенная экспонента

Создадим обобщенную функцию, с помощью которой можно было бы вы­числять значение экспоненты как от действительного числа, так и для ком­плексного аргумента. Комплексные числа будем реализовывать с помощью класса пользователя. Особенность процедуры вычисления состоит в том, что экспонента рассчитывается в виде ряда Тейлора. Весь программный код приведен в листинге 4.1.

Листинг 4.1. Обобщенная экспонента

#include <iostream>

const N=100;

using namespace std;

//Класс для реализации комплексных чисел:

class Complex{

public:

double Re, Im;

//Перегрузка оператора присваивания:

Complex operator=(double x){

Re=x;

lm=0;

return *this;}

//Перегрузка оператора умножения:

Complex operator*(Complex obj){

Complex tmp;

tmp.Re=Re*obj.Re-Im*obj.Im;

tmp.Im=Re*obj.Im+Im*obj.Re;

return tmp;}

//Перегрузка оператора сложения:

Complex operator+(Complex obj){

Complex tmp;

tmp.Re=Re+obj.Re;

tmp.Im=Im+obj.Im;

return tmp;}

//Перегрузка оператора деления:

Complex operator/(double x){

Complex tmp;

tmp.Re=Re/x;

tmp.Im=Im/x;

return tmp;}

} ;

//Шаблонная функция для определения экспоненты:

template Cclass Х> X mExp(X t){

X s;

s=l;

X q=t ; int i;

for(i=l;±<=N;i++){

s=s+q;

q=q*t/(i+1);}}

return s;}

int main(){

Complex z;

z.Re=l;

z. Im=2 ;

cout«"exp ("<<z . Re<<" + "«z . Im<<"i) ="<<mExp (z) . Re<<" + "

<<mExp(z).Im<<"i"<<endl;

cout«"exp (1.0) ="<<mExp (1.0) <<endl ;

cout«"exp (1) ="<<mExp (1) «endl;

return 0;}

Результат выполнения программы имеет следующий вид:

exp(l+2i)=-1.1312+2.47173i exp(1.0)=2/71828 exp(1}=2

Обращаем внимание читателя, что в случае, если аргументом функции ука­зано целое число, то результатом также является число целое. Проблема связана с тем, что для целочисленных операндов по умолчанию операция деления выполняется как деление нацело. Предлагаем читателю самостоя­тельно предложить возможные пути ее решения.

Перегрузка операторов

Рассмотрим пример с перегрузкой операторных функций в обобщенных классах. Пример достаточно простой: в программе объявляется два разных класса А и В. Класс А имеет целочисленное поле к, а класс В имеет поля х и у типа double. В каждом из классов перегружается оператор сложе­ния. Оператор сложения перегружается так, что в результате сложения двух объектов получаем объект того же класса. При этом соответствующие поля объектов складываются. Каждый класс имеет метод show () для ото­бражения значения поля или полей. Также в программе объявляется обоб­щенный класс MyTempl, в котором имеется одно поле res (объект класса А или В). В обобщенном классе MyTempl также перегружается оператор сложения: при сложении объектов класса MyTempl складываются их поля res. Для отображения значений полей объекта-поля res используется ме­тод show (). При его реализации вызывается метод с таким же именем из объекта res. Программный код приведен в листинге 4.2.

Листинг 4.2. Перегрузка операторов

#include <iostream>

using namespace std;

class A{

public:

int k;

A operatorf(A obj){

A tmp ;

tmp . k=k+obj . к; return tmp;}

void show(){

cout<<"k = "<<k<<endl;}

};

class В{

public:

double x,y;

В operatort(B obj){

В tmp;

tmp.x=x+obj.x;

tmp.y=y+obj.y;

return tmp;}

void show(){

cout«"x = "<<x<<endl;

cout«"y = "<<y<<endl; }

};

template <class X> class MyTempl{

public:

X res;

MyTempl operatort(MyTempl obj){

MyTempl tmp;

tmp.res=res+obj.res;

return tmp;}

void show(){

res.show();}

} ;

int main(){

MyTempl<A> al,a2,a3;

MyTempl<B> bl,b2,b3;

al.res.k=l;

a2.res.k=2;

b1.res.x=10.1;

b1.res.y=100.1;

b2.res.x=20.2;

b2.res.y=200.2;

a3=al+a2;

b3=bl+b2;

a3.show ();

b3.show();

return 0;}

В результате выполнения программы получаем:

к = 3

х = 30.3

у = 300.3

Стоит отметить, что поскольку в обобщенном классе метод show () реали­зован через вызов метода show () из объекта res, в качестве типа-параметра X можно использовать только имена классов, в которых объявлен такой ме­тод (и, разумеется, перегружен оператор сложения).