Для малых углов, выраженных в радианах
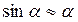 | (7) |
и из (6) – (7) следует:
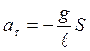 | (8) |
Ускорение является второй производной от смещения, т.е. 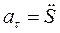 , поэтому:
, поэтому:
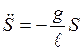 | (9) |
Введем обозначение:
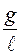 = = 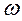 2 2 | (10) |
Подставляя (10) в (9) , получим уравнение движения математического маятника, являющееся однородным дифференциальным уравнением второго порядка:
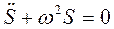 | (11) |
Решение этого уравнения может быть представлено в виде:
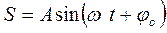 | (12) |
или
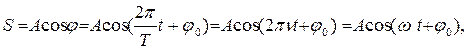 | (13) |
(в этом можно убедиться, непосредственно подставляя (12) в (11)).
Таким образом, колебание маятника является гармоническим (т.е. смещение маятника от положения равновесия меняется с течением времени по закону синуса или косинуса). В формулах (12), (13):
А – амплитуда колебания (модуль наибольшего отклонения колеблющейся величины от равновесного значения S =0);
T – период колебания (время, за которое совершается одно полное колебание);
n = 1/ T – частота колебаний (число колебаний в единицу времени);
w = 2p / Т – циклическая (угловая, круговая) частота (число колебаний за 2p секунд) ;
j = wt + j0 – фаза колебания (выражение, стоящее под знаком синусаили косинуса). Фаза однозначно определяет при заданной амплитуде в любой момент времени значение колеблющейся величины.
j0 – начальная фаза колебания (при t = 0). Слово "фаза" – греческого происхождения, означает ступень, стадию развития какого–либо явления: по значению фазы можно определить, какая часть периода прошла от момента начала колебания: j = 2pt / T (при j0 = 0). Откуда t = jT/(2p) .
Таким образом, период колебаний маятника T = 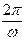 ; где, согласно (10),
; где, согласно (10), 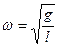 . Или
. Или
T = 2 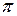 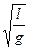 | (14) |
где l – длина математического маятника, g – ускорение свободного падения.
Таким образом, при малых начальных отклонениях от положения равновесия период колебаний математического маятника определяется только его длиной и ускорением свободного падения и не зависит от его массы, а также от начального отклонения от положения равновесия.
С другой стороны , T = 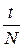 , где t – время N полных колебаний. Эти соотношения могут быть использованы для расчета ускорения свободного падения:
, где t – время N полных колебаний. Эти соотношения могут быть использованы для расчета ускорения свободного падения:
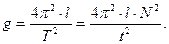 | (15) |
Если измерение длины маятника затруднено, это осложнение легко обойти, измерив периоды колебаний Т1 и Т2 и разность длин маятников ( 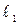 –
– 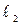 ) в этих экспериментах:
) в этих экспериментах:
T1 = 2 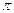 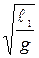 и T2 = 2 и T2 = 2 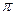 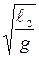 . . | (16) |
Отсюда
g = 4 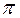 2 2 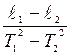 | (17) |
Порядок выполнения работы, обработка результатов измерений:
1. Отклонить маятник от положения равновесия на 5 - 60 и предоставить ему возможность свободно колебаться;
2. Включить секундомер, когда маятник проходит положение равновесия, отсчитать промежуток времени t = 50 полных колебаний. Измерения (t1, t2, t3) повторяют три раза и находят среднее время τ1ср= 50 колебаний при длине маятника l1. Вычисляют абсолютные погрешности отдельных измерений Δτ1, Δτ2, Δτ3 и среднюю абсолютную погрешность Δτ1ср.
3. Разделить τ1ср на n = 50, найти среднее время Т1 одного колебания маятника при длине l 1:
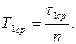 | (18) |
4. Проделать п.п. 1,2,3 при другой длине маятника l2, изменив ее на 12 - 15 см. В этом случае период будет Т2 :
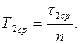 | (19) |
5. Результаты измерений и вычислений записать в таблицу.
6. Пользуясь формулой (17), вычислить g, погрешности.
7. Результаты измерений записывают в виде: 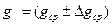 .
.
Таблица
| № п/п | Длина, м | n | τ,с | Τ,с | g, м/с2 | Δg, м/с2 | 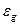 , % , % |
| ср. зн. | |||||||
| ср. зн. |
Контрольные вопросы:
1. Каковы условия возникновения колебаний. Какие колебания называются гармоническими. Назовите основные характеристики гармонического колебания. Какая колебательная система называется математическим маятником.
2. Вывести уравнение движения математического маятника.
3. Вывести формулу периода колебаний математического маятника.
4. Записать решение уравнения движения математического маятника и дать определение всех величин, входящих в данное уравнение.
5. Почему g не определяется непосредственно по формуле для периода математического маятника.
6. Получить расчетную формулу для определения ускорения свободного падения g.
7. Указать силы, действующие на маятник, находящийся в положении равновесия.
Лабораторная работа № 1-2
Определение коэффициента вязкости жидкости методом Стокса
Цель работы: изучение динамики движения тела в вязкой жидкости и экспериментальное определение коэффициента вязкости жидкости.
Оборудование:
1. Сосуд с вязкой жидкостью;
2. Шарики;
3. Микрометр или штангенциркуль;
4. Линейка или мерная лента;
5. Секундомер.
КРАТКАЯ ТЕОРИЯ
Вязкость жидкости– это свойство, характеризующее возникновение сил внутреннего трения при относительном скольжении слоев жидкости, движущихся с различными скоростями, причем сила направлена по касательной к поверхности соприкосновения слоев.
При движении жидкости между её слоями возникают силы внутреннего трения, действующие таким образом, чтобы уравнять скорости всех слоёв.
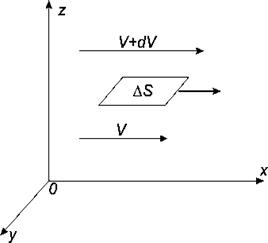
Рис. 1.
Движение жидкости
Природа этих сил заключается в том, что слои, движущиеся с разными скоростями, обмениваются молекулами, что приводит к перераспределению импульсов слоев жидкости. Молекулы из более быстрого слоя передают молекулам более медленного слоя часть импульса, вследствие чего медленный слой начинается двигаться быстрее, а быстрый слой тормозится.
Рассмотрим жидкость, движущуюся в направлении х (рис. 1). Пусть слои жидкости движутся с разными скоростями. На оси 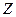 возьмем две точки, находящиеся на расстоянии
возьмем две точки, находящиеся на расстоянии 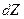 . Скорости потока жидкости отличаются в этих точках на величину
. Скорости потока жидкости отличаются в этих точках на величину 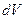 . Отношение
. Отношение 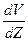 характеризует изменение скорости потока в направлении перпендикулярном направлению скоростей и называется градиентом скорости. При ламинарном течении (т.е. без завихрений) сила внутреннего трения (или вязкости), действующая между слоями, пропорциональна площади их соприкосновения
характеризует изменение скорости потока в направлении перпендикулярном направлению скоростей и называется градиентом скорости. При ламинарном течении (т.е. без завихрений) сила внутреннего трения (или вязкости), действующая между слоями, пропорциональна площади их соприкосновения 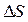 и градиенту скорости (формула Ньютона):
и градиенту скорости (формула Ньютона):
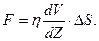 | (15) |
Величина 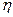 называется коэффициентом внутреннего трения или коэффициентом динамической вязкости. Величина
называется коэффициентом внутреннего трения или коэффициентом динамической вязкости. Величина 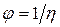 называется текучестью. Если в формуле (1) принять
называется текучестью. Если в формуле (1) принять 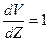 и
и 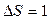 , то
, то 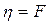 , т.е. коэффициент динамической вязкости численно равен силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения двух слоев, движущихся один относительно другого с градиентом скорости, равным единице.Наряду с коэффициентом динамической вязкости
, т.е. коэффициент динамической вязкости численно равен силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения двух слоев, движущихся один относительно другого с градиентом скорости, равным единице.Наряду с коэффициентом динамической вязкости 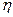 , часто употребляют коэффициент кинематической вязкости
, часто употребляют коэффициент кинематической вязкости 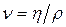 , где
, где 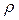 – плотность жидкости. В системе СИ единицей физических величин измерений динамической вязкости
– плотность жидкости. В системе СИ единицей физических величин измерений динамической вязкости 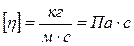 ; кинематической вязкости
; кинематической вязкости 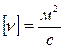 .
.
Коэффициент динамической вязкости 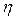 зависит от природы жидкости и для данной жидкости с повышением температуры уменьшается. Слой жидкости, непосредственно прилегающий к твердой поверхности, в результате прилипания остается неподвижным относительно её. Скорость остальных слоев постепенно возрастает по мере удаления от твердой поверхности.
зависит от природы жидкости и для данной жидкости с повышением температуры уменьшается. Слой жидкости, непосредственно прилегающий к твердой поверхности, в результате прилипания остается неподвижным относительно её. Скорость остальных слоев постепенно возрастает по мере удаления от твердой поверхности.
Определение коэффициента вязкости жидкости по методу Стокса:
На всякое тело, движущееся в вязкой жидкости, действует сила сопротивления. В общем случае величина этой силы зависит от многих факторов: от внутреннего трения жидкости, от формы тела, от характера обтекания и т.д. Стоксом было получено строгое решение задачи о ламинарном обтекании шарика безграничной жидкостью. В этом случае сила сопротивления 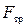 определяется формулой:
определяется формулой:
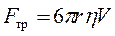 , , | (2) |
где 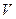 - скорость шарика,
- скорость шарика, 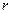 - радиус шарика,
- радиус шарика, 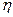 - коэффициент динамической вязкости жидкости.
- коэффициент динамической вязкости жидкости.
Рассмотрим падение шарика в вязкой среде (рис. 1). На шарик действуют три силы:
1. сила тяжести 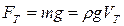 ( ρ – плотность материала шарика,
( ρ – плотность материала шарика, 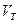
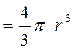 – объем шарика);
– объем шарика);
2. сила Архимеда 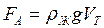 , равная весу жидкости в объеме
, равная весу жидкости в объеме 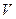 (
( 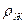 ‑плотность жидкости);
‑плотность жидкости);
3. сила сопротивления со стороны жидкости (сила Стокса) 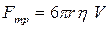 .
.
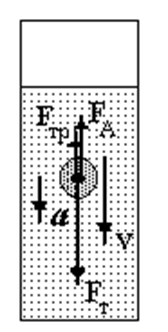
Рис. 2.
Движение шарика в вязкой жидкости
Равнодействующая этих сил обеспечивает шарику, согласно второму закону Ньютона, ускорение:
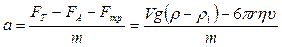 | (3) |
Таким образом, скорость шарика υ с течением времени растет, а следовательно, растет и сила сопротивления 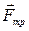 со стороны жидкости, пропорциональная модулю скорости. Когда
со стороны жидкости, пропорциональная модулю скорости. Когда 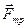 возрастет настолько, что сумма сил
возрастет настолько, что сумма сил 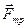 и
и 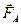 уравновесит силу тяжести
уравновесит силу тяжести 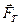 , движение шарика станет равномерным (a = 0), т.е. с постоянной скоростью
, движение шарика станет равномерным (a = 0), т.е. с постоянной скоростью 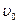 = const.
= const.
Измеряя на опыте установившуюся скорость падения шарика 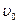 и радиус шарика
и радиус шарика 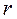 , зная значения плотностей материала шарика
, зная значения плотностей материала шарика 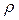 и жидкости
и жидкости 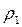 , в которой он движется, можно определить коэффициент внутреннего трения (коэффициент вязкости) жидкости по формуле:
, в которой он движется, можно определить коэффициент внутреннего трения (коэффициент вязкости) жидкости по формуле:
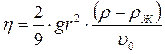 . . | (4) |
Описание установки
Установка (рис.3) состоит из стеклянного цилиндра с исследуемой жидкостью. На поверхности цилиндра имеются две горизонтальные метки, верхняя метка должна быть на 5-10 см ниже уровня жидкости, а нижняя на 5-10 см выше уровня жидкости. Расчетная формула (4) справедлива для безграничной среды, поэтому размеры сосуда должны быть значительно больше размера шарика. По этой же причине шарик должен двигаться как можно ближе к оси цилиндра.
 |
Рис. 3.
Схема установки: (А – верхняя метка (располагается ниже уровня жидкости на 5-10 см), В – нижняя метка располагается выше уровня жидкости на 5-10 см)
