Расчетная модель к теореме Кастильяно

При переходе от состояния 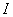балки к состоянию 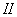все нагрузки Р опустятся, значит, их потенциальная энергия уменьшится. Так как равновесие не нарушалось, то уменьшение, энергии нагрузок 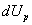целиком преобразовалось в увеличение потенциальной энергии деформаций балки dU. Величина 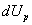измеряется работой внешних сил при переходе балки из положения 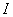в положение II:

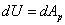
Изменение dU потенциальной энергии деформации, являющейся функцией сил 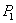, , 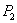,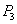..., произошло за счет очень малого приращения одной из этих независимых переменных 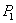, поэтому дифференциал такой сложной функции равен:

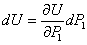
Что касается величины 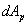, то эта работа в свою очередь является разностью работы нагрузок Р для положений 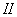и :

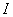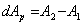
Работа 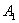при одновременном и постепенном возрастании сил Р равна:

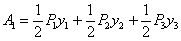
При вычислении работы 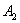учтем, что ее величина всецело определяется окончательной формой деформированной балки и не зависит от порядка, в котором производилась нагрузка.

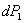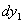
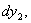
Предположим, что мы сначала нагрузили нашу балку грузом ; балка очень немного прогнется (Рис.2, положение III), и прогибы ее в точках 1, 2, 3 будут 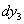. Работа статически приложенной нагрузки 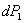будет равна 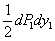. После этого начнем постепенно нагружать балку одновременно возрастающими грузами , , .

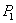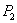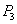Рис.2. Расчетная модель к теореме Кастильяно.

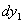
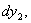
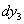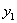
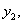
К первоначальным прогибам добавятся прогибы 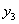(Рис.2). При этой стадии нагружения силы 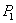, , 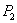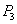произведут работу 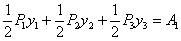, кроме этого, произведет работу уже находившийся на балке груз 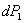; он пройдет путь 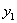, и так как при втором этапе нагружения он оставался постоянным, то его работа равна 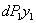Балка займет положение 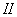, показанное на Рис.2 пунктиром.

Таким образом, полная работа, проделанная внешними нагрузками при переходе балки из недеформированного состояния в положение 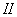, будет равна.

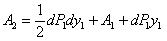
Теперь вычислим

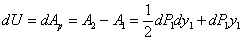
Пренебрегая слагаемым второго порядка малости, получаем:

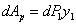
Подставляя полученные значения dU и 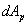в исходное уравнение, находим

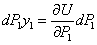
или

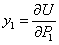
Таким образом, в рассмотренном случае прогиб точки приложения сосредоточенной силы 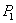, равен частной производной потенциальной энергии деформации по этой силе.

Полученный результат можно обобщить. Пусть на балку помимо сосредоточенных сил Р действуют в разных сечениях еще пары сил М (Рис.3). Мы можем повторить предыдущие рассуждения, считая, что балка переводится из положения 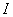в положение 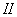путем добавки 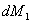к паре 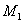. Весь ход рассуждений остается без изменений, надо будет лишь при вычислении работы моментов 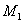, 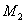... умножать их не на прогибы, а на углы поворота 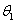, ,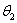... тех сечений, где эти пары приложены. Тогда dU будет равно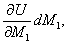 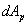станет 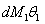, и в итоге получим:

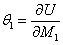
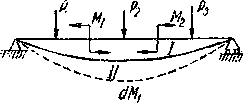
Рис.3. Обобщенная расчетная модель к теореме Кастильяно.

Так как 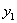— это перемещение, соответствующее силе 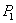, a 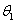— перемещение, соответствующее силе 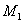то полученные нами результаты можно формулировать так: производная потенциальной энергии деформации по одной из независимых внешних сил равна перемещению, соответствующему этой силе. Это и есть так называемая теорема Кастильяно, опубликованная в 1875 г.

Заметим, что присутствие на балке сплошной нагрузки не меняет предыдущих выводов, так как всякую сплошную нагрузку можно рассматривать как состоящую из большого числа сосредоточенных сил.

Предыдущий вывод был сделан для балки, но совершенно ясно, что его можно повторить для любой конструкции, деформации которой следуют закону Гука.

Для случая изгиба нами была получена формула, связывающая величину потенциальной энергии U с изгибающими моментами:

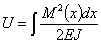
Изгибающий момент является линейной функцией нагрузок 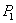, 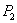…, , 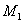,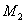..., q, приложенных к балке:

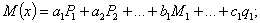
в этом легко убедиться, просмотрев формулы для вычисления изгибающих моментов при построении эпюр. Следовательно, потенциальная энергия является функцией второй степени от независимых внешних нагрузок.

Вычислим частную производную от U по одной из внешних сил, например 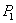. Получаем:

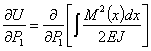
Здесь мы имеем дело с так называемым дифференцированием определенного интеграла по параметру, так как М(х)— функция и 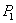и х, интегрирование производится по х, а дифференцирование по параметру 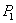. Как известно, если пределы интеграла постоянны, то следует просто дифференцировать подинтегральную функцию.

Таким образом, прогиб в точке приложения сосредоточенной силы 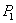равен:

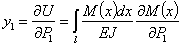
а угол поворота сечения с парой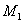

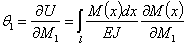
Напомним, что знак предела l условно показывает, что интеграл должен охватить всю балку.