Как называется ряд опытов, проведенных при одних и тех же условиях?

ПОВТОРНЫЕ ИСПЫТАНИЯ.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Индивидуальные задания к модулю 17

Курск 2007

Составитель: Е.В.Журавлева, Е.А.Панина

УДК 519.2

Рецензент

Кандидат технических наук, доцент кафедры

высшей математики Л.В.Карачевцева.

Повторные испытания. Случайные величины. [Текст]: / индивидуальные задания к модулю 17 системы РИТМо по дисциплине «Математика» / сост.: Е.В.Журавлева, Е.А.Панина; Курск. гос. техн. ун-т; Курск, 2007. 53с., табл.1. Библиогр.: 3 назв.

Приведены теоретические упражнения, индивидуальные задания и список рекомендуемой литературы по теме: «Повторные испытания. Случайные величины». Задания разбиты на 3 уровня сложности, выбираемые студентами в зависимости от личной подготовленности.

Предназначены для студентов экономических специальностей.

.

Текст печатается в авторской редакции

ИД №06430 от 10. 12. 2001.

Подписано в печать ________ . Формат 60х84 1/16. Печать офсетная.

Усл. печ. л. Уч.-изд. л. .Тираж 50 экз. Заказ ……. Бесплатно.

Курский государственный технический университет.

Издательско-полиграфический центр Курского государственного технического университета. 305040 Курск, ул. 50 лет Октября, 94.

Содержание

Введение. 4

Теоретические упражнения. 5

Тест 1. 5

Тест 2. 7

Практическая часть. 9

Задание 1. 9

Задание 2. 12

Задание 3. 15

Задание 4. 18

Задание 5. 21

Задание 6. 24

Задание 7. 28

Задание 8. 32

Задание 9. 35

Задание 10. 45

Задание 11. 46

Задание 12. 47

Список используемой литературы………………………………...53

Введение

В целях упорядочения самостоятельной работы студентов при изучении курса «Высшей математики» разработана Рейтинговая Интенсивная Технология Модульного обучения. Эта работа представляет собой один из модулей указанной технологии. Она содержит индивидуальные задания, представляющие собой теоретические упражнения, практические задания, по темам «Повторные испытания», «Случайные величины», «Системы массового обслуживания».

При выборе заданий следует использовать параметр n, где n – номер студента в журнале преподавателя.

При выполнении заданий всем студентам рекомендуется в качестве теоретической подготовки ответить на вопросы теоретических упражнений, разбитых на два варианта (выбор варианта осуществляется по правилу: нечетные варианты выполняют тест 1, четные – тест 2)

В зависимости от уровня подготовки студента рекомендуется воспользоваться тремя уровнями сложности, на которые разбиты задания:

Первый уровень сложности предполагает решение следующих практических заданий – 1, 3, 4, 5, 9, 10.

Второй уровень сложности содержит решение следующих практических упражнений – 1, 3, 4, 5,7, 9,10, 11.

Решение задач третьего уровня сложности практических заданий – 2, 3, 4, 6, 7, 8, 10, 11, 12.

Особо одаренным студентам рекомендуем решить все задания своего варианта.

Теоретические упражнения

Тест 1

Как называется ряд опытов, проведенных при одних и тех же условиях?

2. Если рассматривается последовательность взаимно независимых и одинаковых испытаний, причем в каждом из этих испытаний может наступить событие А с постоянной вероятностью 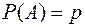, то рассматриваемая схема является схемой Бернулли или схемой Пуассона?

3. Как найти вероятность того, что в n испытаниях (число испытаний мало) событие А наступит m раз?

4. Если р – вероятность наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А в n независимых испытаниях наступит ровно m раз Р_n(m), можно найти используя локальную теорему Лапласа или интегральную теорему Лапласа?

5. Какое название носят величины, значения которых нельзя заранее указать и которые зависят от случайных причин?

6. Если случайная величина может принимать отдельные, изолированные значения, причем их количество конечно или бесконечно, но счетно, то такая величина носит название дискретной, непрерывной или смешанной?

7. Как называется перечень всех значений дискретной случайной величины и их вероятностей?

8. Как находят математическое ожидание дискретной случайной величины: как среднее арифметическое, среднее геометрическое, среднее квадратическое?

9. Перечислите свойства математического ожидания:

1) математическое ожидание постоянной есть сама эта постоянная, ноль или постоянная в квадрате?

2) что получается при вынесении постоянной множителя за знак математического ожидания M[kX]: M[X], k²M[X], kM[X], X?

3) математическое ожидание суммы двух случайных величин равно сумме или произведению математических ожиданий этих величин?

4) если M[X×Y]=M[X]×M[Y], то Х и Y – зависимые или независимые случайные величины?

10. Математическое ожидание отклонения случайной величины Х от его математического ожидания M[X-M[X]] равно нулю, математическому ожиданию M[X] или дисперсии?

11. Перечислите основные свойства дисперсии:

1) дисперсия постоянной величины равна нулю, единице, самой постоянной, постоянной в квадрате?

2) что получается при вынесении постоянного множителя за знак дисперсии D[kX]: D[X], k²D[X], kD[X], X?

3) дисперсия суммы двух величин D[X+Y]=D[X]+D[Y], если Х и Y – зависимые или независимые величины?

12. Как связаны дисперсия D[X] и среднее квадратическое отклонение s[X]: D[X]=s²[X]; D[X]= 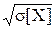; D[X]=s[X]?