Рассмотрим численный пример

В печи необходимо ускоренно нагреть шары радиусом 0,05 м из стали со следующими теплофизическими свойствами: l=25 Вт/(м×К), а=0,55×10^-5 м²/с, коэффициент теплоотдачи в печи a=500 Вт/(м²×К), максимально допустимый перепад по толщине шара из условий прочности для данной стали составляет Dt_доп = 300 °С. Необходимо найти: время достижения максимального перепада температуры по сечению, допустимую температуру печи при посаде шаров с начальной температурой t₀ = 0 °С. При перечисленных исходных данных число Bi=1, проводя линию перпендикулярную оси Bi до пересечения с кривой Fo_max, из рис.1 находим его численное значение, которое составляет 0,116, соответственно максимальный перепад температур сформируется через 53 с. Через точку пересечения перпендикуляра с кривой Dt=300 °С проводим линию, параллельную оси Bi и находим разность t_c – t₀, которая будет соответствовать максимально допустимой температуре среды при нагреве с холодного посада, в нашем случае 976 °С.

Теперь приведём аналитическое решение. Согласно уравнению (10) при коэффициенте геометрической формы k= 3 для шара получим: m=1+1/5=1,2; D=3/1,2=2,5; ρ=D²/525=2,5²/525=0,019; γ ≈1+ρ=1,019 и окончательно первый корень μ₁= 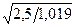=1,5718. Более точно первый корень можно также получить из (17) μ₁=b₁=π/2=1,5708.

Второй корень по формуле (17) при В=1-Вi=0 μ₂ =b₂=3∙π/2=3∙b₁.

Отношения корней δ= (μ₁/μ₂)²=(1/3)²=1/9.

Величины a=μ₂²(1-δ)=9π²/4∙(1-1/9)= 2π²= 19,739. Р₁ согласно (13) Р₁=2/ μ₁²=8/ π²; Р₂=2/ μ₂²=δ∙ Р₁; Е₁=Р₁-А₁= Р₁(1-μ₁/sinμ₁)= Р₁(1- μ₁); Е₂=Р₂(1+μ₂) - т.к. sinμ₁=1, а sinμ₂=-1.

Величина b=-δЕ₁/Е₂=-δ Р₁/(δ Р₁)∙(1-π/2)/(1+3π/2)=0,0999≈0,1.

Окончательно время наступления максимального перепада температур в теле по формуле (6)

Fо_max=1/(2π²)ln(1/0,1)=0,1167.

Максимальный перепад по соотношению (7)

∆Ө_m=(1-1/9)(8/π²)(1-π/2)∙ехр(- π²Fо_max/4)=- 0,3084.

Максимальная разность температур по уравнению (8)

∆t₀=300/(-0,3084)=- 972,8 ⁰С.

Окончательно допустимая температура греющей среды при нагреве шаровых тел t_с.доп= 0- ∆t₀= 973 ⁰С.

Для сравнения с процессами нагрева при Вi=1 плоских и цилиндрических тел результаты аналитических расчетов приведены в табл.5.1.

Таблица 5.1. Максимальное время, перепад температур и допустимая температура печи приВi=1 в зависимости от формы тела

Форма тела	μ1	μ2	а	b	Fomax	-∆Өm	tс.доп, 0С
Пластина	0,8607	3,4257	10,995	0,08	0,2269	0,3084
Цилиндр	0,8929	4,0841	15,883	0,09	0,1509	0,3092
Шар	π/2	3π/2	19,739	0,1	0,1186	0,3084

Из анализа данных табл.5.1 вытекает, что при одном и том же числе Био время наступления максимального перепада уменьшается при переходе от плоских к шаровым телам примерно в 2 раза, а сам перепад температур и предельно допустимая температура греющей среды остаются на одном уровне.

ПЕРЕЧЕНЬ ЛИТЕРАТУРЫ

10.Горбунов А.Д., Шабельник О.М. К расчёту температурных полей и термических напряжений при нагреве плоских тел в движущемся слое / Сб.науч.трудов НМетАУ. – Том 7. – Днепропетровск: 2002. – С. 40–45.

11. Горбунов А.Д. К расчёту термических напряжений при конвективном нагреве пластины // Математичне моделювання. – Днепродзержинск: 2010. № 1(22). – С. 16–21.

12. Горбунов А.Д., Гольдфарб Э. М. Нахождение корней трансцендентных уравнений в задачах теплопроводности пластины при неоднородных граничных условиях // Изв. вузов. Черная металлургия. – 1983. – № 8. – С. 104–108.

13. Горбунов А.Д., Гольдфарб Э. М. Нахождение корней трансцендентных уравнений в задачах теплопроводности цилиндра при неоднородных граничных условиях // Изв. вузов. Черная металлургия. – 1983. – № 12. – С. 94–97.

14. Горбунов А.Д., Гольдфарб Э. М. Нахождение корней трансцендентных уравнений в задачах теплопроводности шара при неоднородных граничных условиях // Изв. вузов. Черная металлургия. – 1984. – № 2. – С. 79–83.

15.Гольдфарб Э.М., Горбунов А.Д. Определение корней трансцендентных уравнений при нагреве тел в прямотоке и противотоке // ИФЖ. – 1984. – Т.46. – № 5. – С. 870–871.

17. Тайц Н.Ю. Технология нагрева стали. – М.: Металлургиздат, 1962. – 567с.

18. Гейтвуд Б.Е. Температурные напряжения. – М.: Изд-во иностранной литературы, 1959. – 350 с.

19. Паркус Г. Неустановившиеся температурные напряжения. – М.: Физматгиз, 1963. – 252 с.

21. Боли Б., Уэйнер Дж. Теория температурных напряжений. –М.: Мир, 1964. – 517с.

22. Коваленко А.Д. Термоупругость. – Киев: Вища школа, 1975. – 216 с.

23.Тимошенко С.П., Гудьер Дж. Теория упругости. – М.: Наука, 1979. – 560с.

28. Тайц Н.Ю. Технология нагрева стали. – М.: Металлургиздат, 1950.–

181 с..

29. Самойлович Ю.А. Температурные напряжения при нагреве массивных тел простейшей формы // Горение, теплообмен, процессы нагрева металла: Сб.науч.тр. ВНИИМТ. – Свердловск: Изд. ВНИИМТ. 1963. № 10. С. 88 − 100.

42. Фридман Я.Б. Механические свойства металлов. Ч.1. Деформация и разрушение. − М.: Машиностроение, 1974. − 472 с.

60. Казанцев Е.И. Промышленные печи. – М.: Металлургия, 1975. – 368 с.

73. Золоторевский В.С. Механические свойства металлов.–М.: Металлургия, 1983. – 352 с.

105. Тылкин М.А., Яловой Н.И., Полухин П.И. Температуры и напряжения в деталях металлургического оборудования. – М.:Высшая школа, 1970. – 428 с.

106. Тайц Н.Ю., Янковский М.И., Иванченко И.Ф. Температурные напряжения при нестационарных тепловых процессах // Изв.вуз. Черная металлургия. 1969. № 6. С. 149 – 153.

107. Тимофеев В.Н., Самойлович Ю.А., Стрельцов А.К. Экспериментальное исследование температурных деформаций в стальном образце методом электротензометрии // Горение, теплообмен, процессы нагрева металла: Сб.науч.тр. ВНИИМТ. – Свердловск: Изд. ВНИИМТ. 1963. № 10. С. 81 − 87.

118. Стариков В.С. К вопросу разрушения стальных заготовок от температурных напряжений // Изв.вуз.Черная металлургия.1966.№ 11.С.158-163.

126. Лыков А.В., Теория теплопроводности. – М.: Высшая школа,1967.600 с.

140. Маковский В.А., Лаврентик И.И. Алгоритмы управления нагревательными печами. − М.: Металлургия, 1977. – 183 с.

152. Губа В.М., Постольник Ю.С., Гаранчук В.А. Приближенный расчет температуры и напряжений в телах простой формы при конвективном нагреве // Изв. вузов Черная металлургия.-1972. №3.

160. Сабельников А.Г., Тайц Н.Ю. Термоупругие напряжения в сплошном шаре // Изв. вузов Черная металлургия.-1976. №1.

193.Мелан Э., Паркус Г. Термоупругие напряжения, вызываемые стационарными температурными полями. – М.: Физматгиз,1958.–167 с.

199.Постольник Ю.С. Приближенные методы исследований в термомеханике. – К. – Донецк: Вищ. шк., 1984. – 158 с.

200.Постольник Ю.С., Огурцов А.П. Металургійна термомеханіка. – Дніпропетровськ: Системні технології, 2002. – 633 с.