Проверка адекватности модели

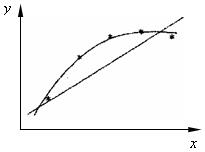 Проверка гипотезы об адекватности осуществляется путем сравнения разброса опытных данных относительно уравнения регрессии с величиной случайной ошибки эксперимента. Если разброс того же порядка, что и ошибка опыта, то его можно объяснить случайными ошибками: уравнение адекватно. Если разброс значительно больше, то он, очевидно, не сводится к ошибке опыта, а связан с неадекватностью уравнения. Уравнения нужно усложнить. Так, с помощью метода наименьших квадратов на рис. 8.4 через одни и те же точки проведены прямая и парабола. Прямая неадекватна, а парабола адекватна.
Проверка гипотезы об адекватности осуществляется путем сравнения разброса опытных данных относительно уравнения регрессии с величиной случайной ошибки эксперимента. Если разброс того же порядка, что и ошибка опыта, то его можно объяснить случайными ошибками: уравнение адекватно. Если разброс значительно больше, то он, очевидно, не сводится к ошибке опыта, а связан с неадекватностью уравнения. Уравнения нужно усложнить. Так, с помощью метода наименьших квадратов на рис. 8.4 через одни и те же точки проведены прямая и парабола. Прямая неадекватна, а парабола адекватна.
Для количественной оценки вводится мера разброса данных дисперсия. Мерой разброса опытных данных относительно модели является остаточная дисперсия 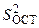 , равная отношению минимальной суммы квадратов отклонений S к числу степеней свободы.
, равная отношению минимальной суммы квадратов отклонений S к числу степеней свободы.
Числом степеней свободы называют разность между числом экспериментов и числом неизвестных параметров, оцениваемых на основании этих экспериментов. Окончательно, выражение для остаточной дисперсии
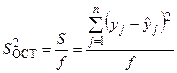 , , | (8.15) |
где f число степеней свободы ( 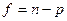 ; n – число экспериментов; р – число оцениваемых параметров).
; n – число экспериментов; р – число оцениваемых параметров).
Для оценки величины случайной ошибки эксперимента рассчитывают дисперсию воспроизводимости 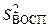 . Для этого проводят одну или несколько серий параллельных опытов; в каждой такой серии значения входных переменных от опыта к опыту не меняются. В этом случае отклонения относят к среднему значению измеряемой величины. А число степеней свободы будет на единицу меньше числа параллельных опытов m.
. Для этого проводят одну или несколько серий параллельных опытов; в каждой такой серии значения входных переменных от опыта к опыту не меняются. В этом случае отклонения относят к среднему значению измеряемой величины. А число степеней свободы будет на единицу меньше числа параллельных опытов m.
Формула 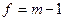 объясняется в данном случае так же, как и формула для f при описании уравнениями: единица наименьшее число опытов, необходимое для того, чтобы составить представление о среднем значении определяемой величины
объясняется в данном случае так же, как и формула для f при описании уравнениями: единица наименьшее число опытов, необходимое для того, чтобы составить представление о среднем значении определяемой величины
Итак
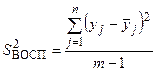 , , | (8.16) |
где 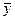 – среднее значение у всех результатов экспериментов.
– среднее значение у всех результатов экспериментов.
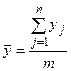 , , | (8.17) |
Для проверки адекватности рассчитывают дисперсионное отношение F
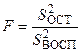 , , | (8.18) |
Если F больше некоторого критического значения, то уравнение неадекватно, если меньше, то адекватно. Критическое значение F зависит от двух чисел степеней свободы: 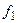 , входящего в формулу (8.15),
, входящего в формулу (8.15), 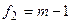 , входящего в формулу (8.16).
, входящего в формулу (8.16).
Чем меньше 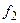 , тем больше критическое F: чем меньше число степеней свободы при оценке дисперсии воспроизводимости, тем эта оценка менее точна и тем менее определенно приходится оценивать адекватность: не исключено, что даже очень большой разброс объясняется ошибкой опыта. Во всяком случае для оценки
, тем больше критическое F: чем меньше число степеней свободы при оценке дисперсии воспроизводимости, тем эта оценка менее точна и тем менее определенно приходится оценивать адекватность: не исключено, что даже очень большой разброс объясняется ошибкой опыта. Во всяком случае для оценки 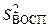 целесообразно провести не менее трех опытов (
целесообразно провести не менее трех опытов ( 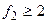 ).
).
