Рассмотрим действия, которые задают функции перехода

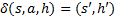- замена символа.

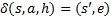- чтение символа h из вершины магазина.

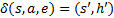- запись 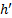в магазин.

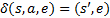- переход МА в состояние .

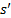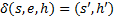- замена символа в вершине.

Конфигурация в которой используется начальное состояние магазинного автомата и на входной ленте записана полная входная цепочка, эта конфигурация начальная 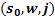- начальная конфигурация, 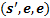- заключительная конфигурация.

Цепочка 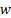называется допустимой для магазинного автомата, если существует последовательность конфигураций этого автомата, первая из которых является начальной, а последняя заключительной .

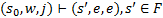Множество цепочек, допускаемых МА называется языком, допускаемым этим автоматом.

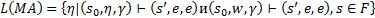
12. Магазинный автомат: способы задания функции переходов МА.

Способ задания функций перехода магазинного автомата

1) Перечисление значений;

2) Таблица переходов;

3) Диаграмма переходов

Рассмотрим пример МА, функция перехода которого задается таблицей переходов.

S0	S1
S/Pi	a	b	a	b	e
a
b
h0

Т.о. размер таблицы переходов зависит от числа состоянии. Если входной символ n, магазинный символ m, число состояний L,то размерность таблицы n*m*L.

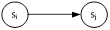
входной символ>, <символ магазина>/<цепочка в магазине>

13. Магазинный автомат: построение МА для заданной грамматики. Для каждой контекстно свободной грамматики можно построить МА, который допускает язык совпадающий с языком, порождаемым заданной грамматикой.

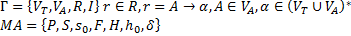
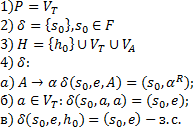
Начальная конфигурация: 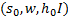, где 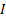- н.с.

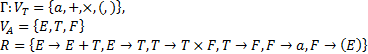
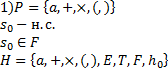
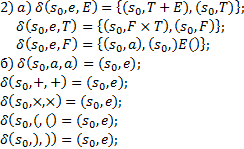
14. Магазинный автомат: построение детерминированных нисходящих распознаваний Работа недетерминированных распознавателей задана поиском последовательности переходов из начальной конфигурации в заключительную. Такой поиск может быть весьма трудоемким, поэтому для построения реальных устройств или программ, моделирующих работу распознавателей желательно использовать детерминированные модели. Согласно предыдущему варианту построения нисходящего распознавания и появлению в вершине магазина не терминала его следует заменить цепочкой, которая представляет собой правую часть какого-либо правила для рассматриваемого не терминала, если левые части всех правил заданной грамматики различны, то распознаватель будет детерминированным (так как каждому не терминалу в вершине магазина соответствует единственная цепочка).Класс грамматик у которых все левые части различны очень узок, поэтому рассмотрим другой класс грамматик у которых все правила начинаются с терминалов: .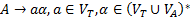

КС грамматика без пустых правил называется разделенной или простой, если выполняются следующие два свойства:

1) Правая часть каждого правила начинается с терминала;

2) Если два правила имеют одинаковые левые части, то правая часть начинается разными терминальными символами;