Производная сложной функции
Пример
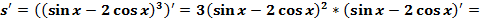
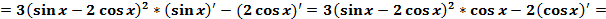
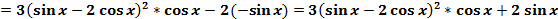
31) Основные теоремы дифференциального исчисления. Правило Лопиталя.
1) Основные теоремы дифференциального исчисления:
1.1) (ax)’ = a(x)’
1.2) (u+v)’ = u’ + v’
1.3) (u*v)’=u’*v+u*v’
1.4) (u/v)’= 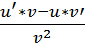
2) Правило Лопиталя используется для раскрытия неопределённостей вида  или
или  при вычисления пределов.
при вычисления пределов.
Теорема (Правило Лопиталя) Если функции f(x) и g(x) дифференцируема в некоторой точке 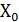 и ее окрестности и существуют пределы
и ее окрестности и существуют пределы
Lim f’(x) и Lim g’ (x),
x-> 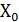 x->
x-> 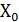
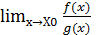 =
= 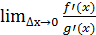
37) Понятие функции нескольких переменных. Частные произведения 1-гопорядка ФНП. Полный дифференциал ФНП. Частные произведение высших порядков ФНП.
Если каждой точке М(х,у) ? D ставится в соответствие единственное число Ƶ=(x,y),то говорят что на множестве D задана функция двух переменных
Множества D называется областью определения функции Ƶ(это все точки с координатами (х,у) которые можно подставить в формуле и получить Ƶ)
Множество Е-называется областью значении (это все значения Ƶ которые получаются).
Ƶ=f(x,y)
Функция многих переменных
Производная первого порядка функции многих переменных

Частной производной по переменной х функции Ƶ=f(x,y) называется предел
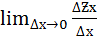
Обозначается производной: 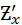 или
или 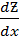
Частной производной по у называется
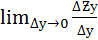
Обозначается : 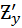 или
или 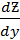
Пример: найти частные производные 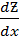 и
и 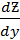 функции
функции
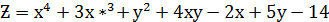
Решение
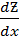 =
= 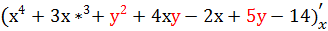 =
= 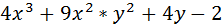
0-0= 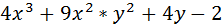
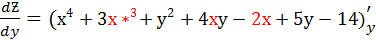 =
= 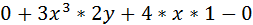
5-0= 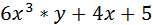
Производная ФМП высшего порядка
Определение:Частными производными второго порядка функции Ƶ=f(x,y) называются частные производные ее частных производных
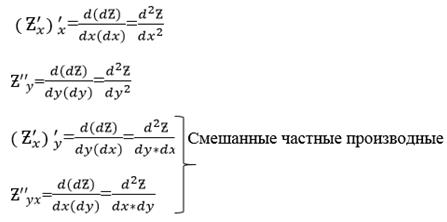
Найти частные производные второго порядка
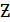 =
= 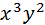
Решение:
1.Найдем 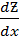 и
и 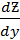
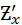 =
= 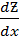 =
= 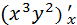 =
= 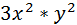
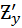 =
= 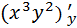 =
= 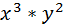
2.Найдем 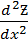 ;
; 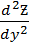 ;
; 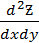 ;
; 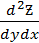
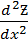 =
= 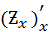 =
= 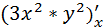 =
= 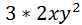 =6x
=6x 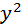
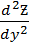 =
= 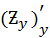 =
= 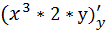 =
= 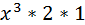 =2
=2 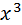
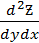 =
= 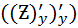 =
= 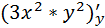 =
= 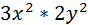 =6
=6 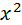 y
y
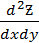 =
= 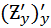 =
= 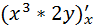 =
= 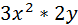 =6
=6 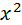 y
y
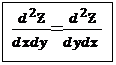 Теорема: (Шварца)
Теорема: (Шварца)
Монотонность и экстремумы функций. Признак монотонности функции. Необходимое и достаточное условие экстремума.
Монотонность
Если функция f(x) непрерывна и имеет производную на интервале (а,в), то функция f(x) – возрастает (убывает) на (а,в) если f’(x)>0 (f’(x)<0) на (а,в)
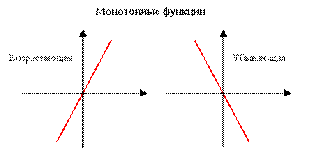
Замечание: промежутки возрастания и убывания называются промежутками монотонности
Экстремум
Определение: Точка 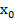 -точка максимума функции на (а,в) если для vxe(a,в) f(
-точка максимума функции на (а,в) если для vxe(a,в) f( 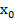 )>f(x)
)>f(x)
Определение: Точка 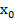 -точка минимума f(x) на (а,в) если для vxe(a,в) f(
-точка минимума f(x) на (а,в) если для vxe(a,в) f( 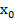 )<f(x)
)<f(x)
Определение: Точки, в которых производна функции f(x) равно нулю или не существует называются критическими
Если f’(x) проходя через критическую точку 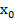 меняет свои знак с:
меняет свои знак с:
А) «+» на «-», то 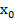 -точка max
-точка max
Б) «-» на «+», то 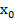 -точка min
-точка min
Определение: Значение функции в точках max и min называется экстремумом функции.
35. Выпуклость и перегиб.
Определение:
 График функции f(x) называется выпуклым вверх на интервале (a,b) находятся выше.
График функции f(x) называется выпуклым вверх на интервале (a,b) находятся выше.
 График функции f(x) называется выпуклым вниз, если все касательные ниже.
График функции f(x) называется выпуклым вниз, если все касательные ниже.
 Точки функции f(x) в которых меняет перегиб f(x) называется точками перегиба.
Точки функции f(x) в которых меняет перегиб f(x) называется точками перегиба.
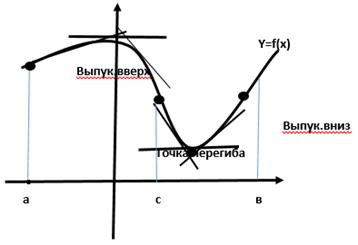
Теорема
Если F’’ (x)< 0 на (a,b), то график функции f(x) на этом интервале имеет выпуклость вверх.
Если F’’ (x)>0, то F(x) – выпуклость вниз на (а,в)
Определение:
Если проходя через точку 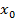 F’’(x) меняет знак С “+” на “-“ или наоборот, т
F’’(x) меняет знак С “+” на “-“ или наоборот, т 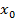 - точка перегиба
- точка перегиба
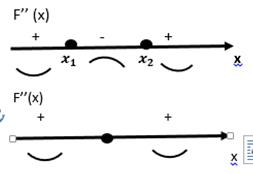
Пример:
Исследовать на выпуклость и точки перегиба график функции y= 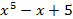
Решение:
1. Найдем у’’
Y’ = ( 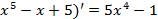
Y’’ = (5 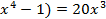
2. Найдем точки в которых F’’(x)=0
20 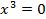
X=0
3. Найдем знаки F’’(x) на промежутках и определим интервалы выпуклости и точки перегиба
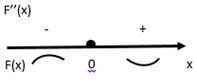
X=0 – точка перегиба
x 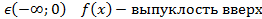
x 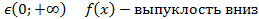
Понятие первообразной, понятие неопределенного интеграла. Свойства неопределенного интеграла. Таблица неопределенных интегралов.
