Построение компьютерной модели расчёта

Траектории неуправляемого ЛА (с заданными характеристиками)

Анализ и представление исходных данных

Эта часть курсового проекта посвящена разработке компьютерной модели расчета траектории неуправляемого летательного аппарата, используя методы численного интегрирования Эйлера и Рунге-Кутта, а также расчету траектории пассивного участка полета неуправляемого ЛА с использованием параболической теории.

В общем случае, траектория полета неуправляемого ЛА состоит из следующих характерных участков:

· движение по направляющим;

· активный участок;

· пассивный участок.

Расчетные соотношения:

Секундный массовый расход (Q) рассчитан по формуле: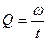

Реактивная сила R рассчитана по формуле: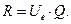

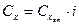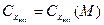Коэффициент лобового сопротивления Cx рассчитан по формуле: , где – коэффициент лобового сопротивления эталонного ЛА.

Площадь миделя ЛА рассчитана по формуле: .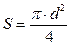

После подстановки исходных данных, соответствующих номеру варианта, в расчётные соотношения, заполняется таблица 2.

Таблица 2

Секундный массовый расход Q, кг/с	Реактивная сила R, Н	Площадь миделя S, м2	Среднее значение коэффициента лобового сопротивления Cx
		0.0113	0.289

Модель динамики неуправляемого ЛА

Движение ЛА по направляющим

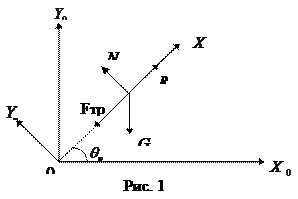Для решения системы дифференциальных уравнений движения ЛА необходимо найти скорость схода и время схода с направляющих: v и t. Направляющая считается абсолютно жесткой, неподвижной, прямолинейной. Из-за малости скорости движения пренебрегают силой лобового сопротивления, учитывают силу трения.

Примем коэффициент трения f_тр=0.15 (для стали), расходом топлива при движении по направляющим пренебрегаем.

В общем случае, уравнение движения ЛА по направляющим (см рис. 1):

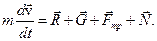
Уравнения в проекциях оси координат направленные вдоль и перпендикулярно направляющим имеет вид:

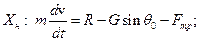
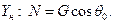
Причем 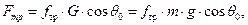где 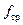– коэффициент трения ЛА об оси направляющих.

Перепишем уравнение в виде:

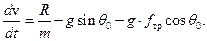
В нашем случае m=m_н=const. Тогда мы имеем:

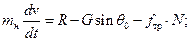
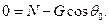
Отсюда находим

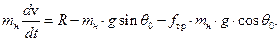
Далее вычисляем

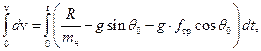
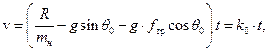
где

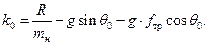
С учетом 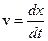получаем

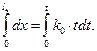
Отсюда находится t₀ через длину направляющей l_н:

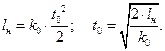
Результаты расчета движения по направляющим приведены в таблице 3.

Таблица 3

Скорость vд, м/с	Время tд, с
22.7084	0.2202

Активный участок

Запишем уравнение движения в векторной форме:

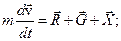
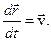
Проекции на касательную и нормаль к траектории уравнения движения:

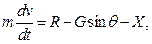
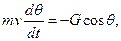
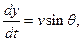
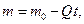
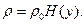
Система из четырех нелинейных дифференциальных уравнений первого порядка относительно четырех переменных 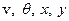решается численно с начальными условиями конца схода с направляющих: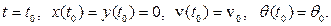

Начальными условиями интегрирования системы являются конечные значения расчёта схода ЛА с направляющей: Условие окончания интегрирования является время горения топлива, т.к. так после завершения горения топлива прекращается действие реактивной силы и ЛА переходит в движение на пассивном участке.

Пассивный участок

Рассмотрим уравнения движения в проекциях на касательную и нормаль траектории:

,

,

,

,

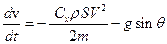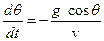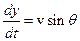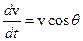Эта система уравнений интегрируется при следующих начальных условиях:

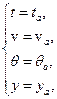
где индекс «а» обозначает конец активного участка. Конечные значения активного участка становятся начальными значениями пассивного участка. Условие окончания интегрирования: y = 0.

При расчете пассивного участка полета ЛА используется ряд допущений, а именно:

· Реактивная сила R равна нулю (R=0).

· Поверхность Земли представляется в виде бесконечной плоскости.

· Масса ЛА постоянна ( 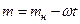=const).