Исходные данные, средние значения измеренных направлений и элементы приведения
| X2= У2= | 6323522,15 м 11411148,18 м | Пункт Наблюде-ния | Направ-ление | Измер. направ. º ' '' | Элементы приведения | |||||||
| Система координат | 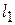 = | 0,225 | м. | |||||||||
| Государственная 1942 г. | 50,9 | 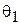 = | 120º | 18' | ||||||||
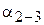 = | 64° 59¢ 42,5² | 23,5 | на пункт 6 | |||||||||
| B2-3= | 2470,483 м | 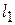= | 0,012 | м. | ||||||||
| B4-5= | 2245,067 м | 35,4 | 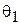= | 160º | 00’ | |||||||
| 39,2 | на пункт 3 | |||||||||||
| 27,4 | ||||||||||||
| 18,3 | ||||||||||||
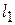| = | 0,003 | м. | ||||||||||
| 23,1 | 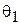= | 241º | 00' | |||||||||
| 16,6 | на пункт 5 | |||||||||||
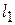| = | 0,015 | м. | ||||||||||
| 04.0 | 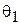= | 270º 00’ | ||||||||||
| 15,9 | на пункт 4 | |||||||||||
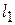| = | 0,563 | м. | ||||||||||
| 44,1 | 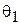= | 104º | 30' | |||||||||
| 00,9 | 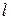 = | 0,015 | м. | |||||||||
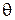 = | 50º | 30' | ||||||||||
| на пункт 1 | ||||||||||||
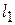| = | 0,076 | м. | ||||||||||
| 53,8 | 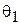= | 17º | 00' | |||||||||
| 59,5 | на пункт 1 | |||||||||||
| 36,1 | ||||||||||||
| 23,6 | ||||||||||||
| 36,1 | ||||||||||||
Для вычисления углов в треугольниках используют измеренные направления на пунктах сети триангуляции. Для примера рассмотрим треугольник под номером I, который образован углами 1, 2, 3.
Значение углов в треугольнике вычисляются по формулам :
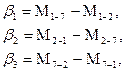(2)
где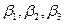 
- значения углов в треугольнике; 
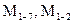- значения направлений, измеренных на пункте 1, 
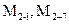- значения направлений, измеренных на пункте 2, 
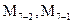- значения направлений, измеренных на пункте 7.
Пример.
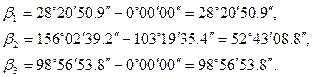
Аналогично вычисляются углы в других треугольниках. Значения вычисленных углов записывают в таблицу 4.
Предварительное решение треугольников
Для вычисления поправок в измеренные направления за центрировку теодолита и редукцию визирных целей на пункте необходимо вычислить длины сторон треугольников.
При решении треугольников целесообразно придерживаться следующих рекомендаций:
¾ в каждом треугольнике на первом месте выписывается номер вершины того угла, который лежит против исходной стороны, а на последнем – против стороны, которая служит исходной при решении следующего треугольника;
¾ вычисляют сумму измеренных углов и невязку в треугольнике.
В треугольнике с углами А, В, С длины противолежащих сторон, соответственно a, b, c, вычисляют по теореме синусов углов:
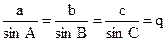, (3)
если известно значение стороны a, то длины других сторон находят по формулам: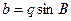 
, 
.
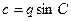Длины сторон вычисляют до метров и записывают в таблицу 4.
В нашем примере вычисления начинают с треугольника II, в котором сторона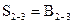 
является базисной, ее значение берется из таблицы 1. Сторона расположена против вершины 7, в таблицу записываем ее первой. Сторона 
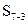будет исходной для вычисления длин в треугольнике III, поэтому записываем ее последней. Вычисления производим по формулам (3), округляя результат до целых метров.
Пример.
,
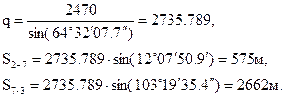Контролем решения треугольников является сходимость дважды вычисленной длины стороны сети. В рассматриваемом примере это сторона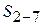 
, вычисленная дважды во II и I треугольниках.
В таблице 4 вычисляются предварительные невязки в треугольниках для контроля грубых ошибок. При вычислении невязки сумма углов в треугольнике сравнивается с теоретической суммой, равной 1800.
Вычисления производят по формуле:
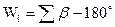, (4)
где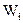 
- невязка 
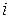- того треугольника; 
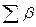- сумма углов, образующих треугольник.
Невязки в угловых секундах вписывают в соответствующие поля таблицы 4.
Например для треугольника II.
Пример.
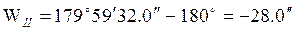
Таблица 4