Ренты, выплачиваемые несколько раз в год

Ежегодные ренты встречаются значительно реже, чем ренты, выплачиваемые несколько раз в год. Так, например, пенсии выплачиваются ежемесячно. Страховые премии также часто вносятся ежемесячно или ежеквартально. Принципы расчета текущей стоимости этих рент такие же, как и в случае ежегодных рент, однако вывод окончательных формул более сложен в связи с тем, что необходимо уметь вычислять дисконтные множители и численность доживающих для интервалов времени, длительность которых менее года. Для дисконтных множителей мы предполагаем, что наращивание процентов происходит непрерывно; для промежуточных же значений численности доживающих используется линейная интерполяция .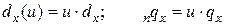

Рассмотрим авансированную срочную ренту, выплачиваемую 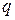раз в год. Величина каждой выплаты равна 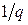, поэтому суммарная выплата за год, как и в случае ежегодной ренты, равна единице.

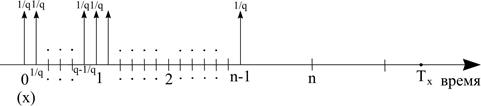
Текущая стоимость этой ренты обозначается так же, как и для ежегодной ренты, но с верхним индексом :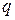

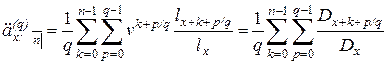. (1)

Простые формулы для 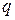-кратных рент

Если значение годовой процентной ставки достаточно мало, то можно считать, что линейная интерполяция справедлива не только для числа доживающих, но и для дисконтного множителя (т.е. в пределах года начисление процентов происходит по закону простых процентов). Тогда и для коммутационной функции 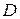также будет справедлива линейная интерполяция в пределах года:

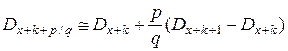. (2)

Подставим формулу (2) в формулу (1) и выполним суммирование по :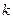

;

.

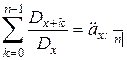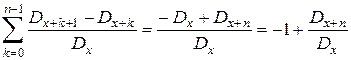Затем выполним суммирование по 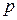с использованием формулы для суммы членов арифметической прогрессии:

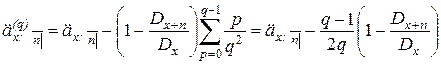. (3)

Аналогичным образом можно получить и формулу для обычной ренты

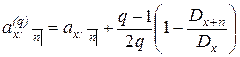. (4)

Если процентная ставка достаточно велика, то линейная интерполяция (2) для 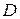неприменима, и требуется более детальный анализ.

Точные формулы для 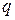-кратных рент для произвольной процентной ставки

Если процентная ставка достаточно велика, то линейная интерполяция (2) для 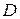неприменима. Поэтому будем использовать в расчетах линейную интерполяцию только для числа доживающих ( 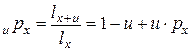), для дисконтных же множителей будем использовать точные выражения. В результате получим

;

,

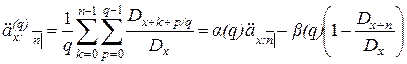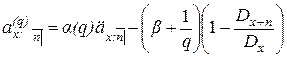где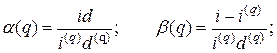

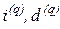– фактические процентная и учетная ставки за период, равный 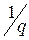части года, определяемые формулами

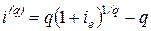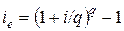; (эффективная процентная ставка);

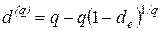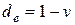; (эффективная годовая учетная ставка).

Непрерывные ренты

Если выплаты ренты происходят достаточно часто, то можно считать, что процесс выплаты рент непрерывен (особенно для еженедельных выплат). Текущую стоимость непрерывной ренты легко получить из формул (3) или (4) при :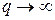

.
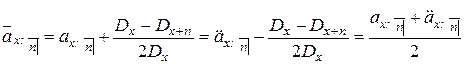