Частотные характеристики Дискретной случайной величины
Определение
Случайная величина — это величина, которая принимает в результате опыта одно значение из множества исходов, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать
Классификация
Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством)
Для сравнения - непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.
Непрерывной называют случайную величину, которая может принимать любые значения из некоторого заданного интервала, например, время ожидания транспорта, температура воздуха в каком-либо месяце, отклонение фактического размера детали от номинального, и т.д. Интервал, на котором она задана, может быть бесконечным в одну или обе стороны.
Если случайная величина не относится ни к дискретным, ни к непрерывным случайным величинам, то ее называют смешанной
Ф-я распределения для дискретных и случайных величин в общем виде
Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x:
F(X) = P(ξ < X).
Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины. Ниже будет приведён пример, разъясняющий смысл сказанного.
Вероятность того, что случайная величина Х принимает значение меньшее х , называется функцией распределения случайной величины Х и обозначается F ( x )

Функция распределения дискретной случайной величины
Если x - дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями p1 < p2 < … < pi < …, то таблица вида

называется распределением дискретной случайной величины.
Функция распределения случайной величины, с таким распределением, имеет вид
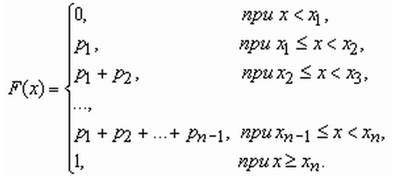
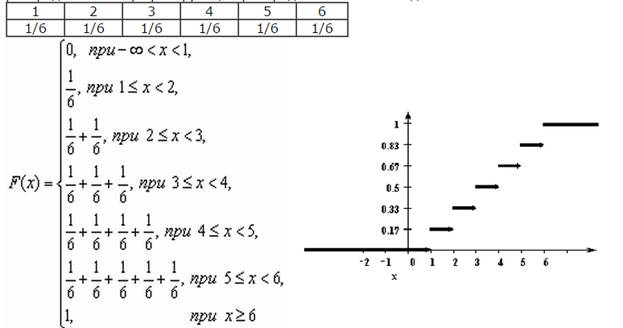
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:
Функция распределения и плотность вероятности непрерывной случайной величины
Если функция распределения Fx (x) непрерывна, то случайная величина x называется непрерывной случайной величиной.
Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величиныpx(x), которая связана с функцией распределения Fx (x) формулами
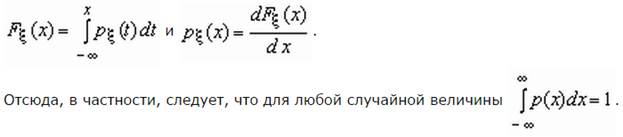
Частотные характеристики Дискретной случайной величины
Математическое ожидание случайной величины
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: М(X) 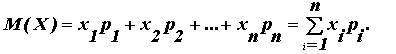
Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины. Равенство будет тем точнее, чем больше число испытаний.
