Элементы функциональной полноты в классе двоичных функций
Основные двоичные функции и их своства.
Булевой функцией f(x1 … xn) называют функцию, аргументы которой принимают значения из множества , и значение функции также из множества {0;1}.
1.Табличные способы задания булевых функций :
| x1 | … | xn | F(x1…xn) |
| … | * | ||
| … | * | ||
| … | … | … | … |
| … | * |
В начале выписываются двоичные наборы из n нулей и единиц. Это удобно делать в двоичной системе счисления – то есть начиная с нуля прибавлять единицу в двоичной системе счисления. На каждом наборе надо задать значение функции.
Пример табличного задания функции:
| x1 | x2 | x3 | f(x1 x1 x3) |
2.Основные булевые функции и их таблицы.
0 – константа ноль ;
1 – константа один ;
x - тождественная ;
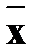 - отрицание ;
- отрицание ;
 - конъюнкция (логическое умножение) ;
- конъюнкция (логическое умножение) ;
 - дизъюнкция (логическое сложение) ;
- дизъюнкция (логическое сложение) ;
+ - модульная сумма ;
~ - эквивалентность (отрицание модульной суммы) ;
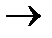 - следствие .
- следствие .
| x1 | x2 | x1 | 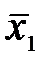 | x1  x2 x2 | x1  x2 x2 | x1+ x2 | x1 ~ x2 | x1 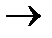 x2 x2 | ||
3.Свойства булевых функций :
Определения.
Бинарная операция 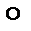 ассоциативна, если тождественно выполняется:
ассоциативна, если тождественно выполняется: 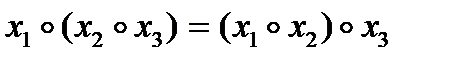 ;
;
бинарная операция коммутативна, если тождественно выполняется: 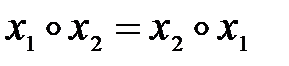 ;
;
бинарная операция 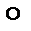 дистрибутивна по отношению к бинарной операции
дистрибутивна по отношению к бинарной операции  , если тождественно выполняется:
, если тождественно выполняется:
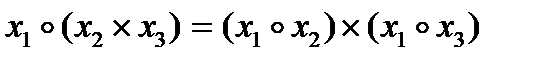 ;
;
Утверждение 1. 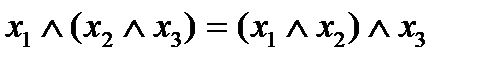 , конъюнкция ассоциативна.
, конъюнкция ассоциативна.
| x1 | x2 | x3 | x2  x3 x3 | x1  (x2 (x2  x3) x3) | x1  x2 x2 | (x1  x2) x2)  x3 x3 |
| 1 | 1 |
Утверждение 2. 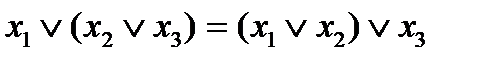 ,
,
дизъюнкция ассоциативна.
| x1 | x2 | x3 | x2  x3 x3 | x1  (x2 (x2  x3) x3) | x1  x2 x2 | (x1  x2 ) x2 )  x3 x3 |
| 1 | 1 |
Утверждение 3. 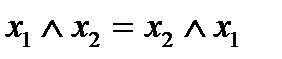 , конъюнкция
, конъюнкция
коммутативна; 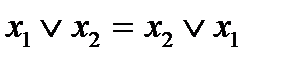 , дизъюнкция также
, дизъюнкция также
коммутативна;
| x1 | x2 | x1  x2 x2 | x2  x1 x1 |
| 1 | 1 |
Предложение 1. Результат выполнения ассоциативной операции не зависит от расположения скобок в скобочном выражении.
Например: Если 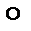 ассоциативная операция, тогда
ассоциативная операция, тогда
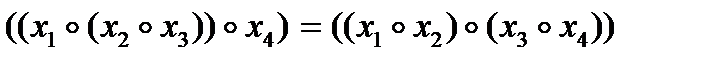 .
.
Доказательство предлагается в качестве домашнего упражнения.
Примечание: использовать индукцию по числу скобок в выражении.
Из того, что конъюнкции и дизъюнкции ассоциативные операции, результат конъюнкции или дизъюнкции нескольких переменных не зависит от расположения скобок.
Например: 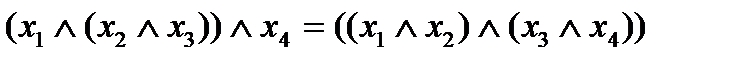
Тогда в силу независимости значения выражений конъюнкций от расположения скобок корректно определение 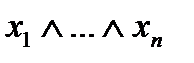 как значение логического произведения при каком-либо порядке расположения скобок. Точно также для дизъюнкции
как значение логического произведения при каком-либо порядке расположения скобок. Точно также для дизъюнкции 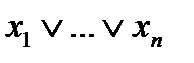 .
.
Предложение 2. Конъюнкция 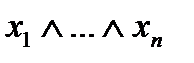 равна 0, т. и т.т., когда хотя бы один из множителей
равна 0, т. и т.т., когда хотя бы один из множителей 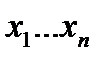 равен 0.
равен 0.
Дизъюнкция 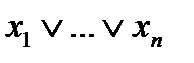 равна 1, т. и т.т., когда хотя бы одно из слагаемых
равна 1, т. и т.т., когда хотя бы одно из слагаемых 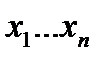 равно 1.
равно 1.
Доказательство предлагается в качестве домашнего упражнения.
Утверждение 4.
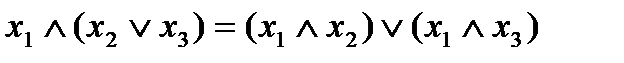 , конъюнкция дистрибутивна по отношению к дизъюнкции.
, конъюнкция дистрибутивна по отношению к дизъюнкции.
| x1 | x2 | x3 | x2  x3 x3 | x1  (x2 (x2  x3) x3) | x1  x2 x2 | x1  x3 x3 | (x1  x2 ) x2 )  (x1 (x1  x3 ) x3 ) |
| 1 | 1 |
Утверждение 5.
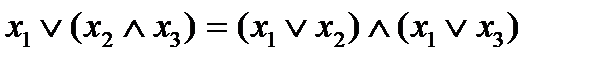 , дизъюнкция дистрибутивна по отношению к конъюнкции.
, дизъюнкция дистрибутивна по отношению к конъюнкции.
| x1 | x2 | x3 | x2  x3 x3 | x1  (x2 (x2  x3) x3) | x1  x2 x2 | x1  x3 x3 | (x1  x2) x2)  (x1 (x1  x3) x3) |
| 1 | 1 |
Утверждение 6. 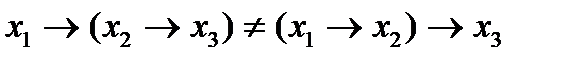 , следствие не ассоциативная операция.
, следствие не ассоциативная операция.
| x1 | x2 | x3 | x2 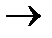 x3 x3 | x1 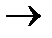 (x2 (x2 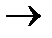 x3) x3) | x1 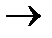 x2 x2 | (x1 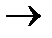 x2) x2) 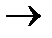 x3 x3 |
| 0 | ||||||
| 1 | 1 |
Утверждение 7. 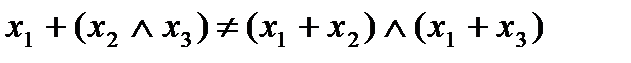
| x1 | x2 | x3 | x2  x3 x3 | x1 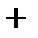 (x2 (x2  x3) x3) | x1+x2 | x1+x3 | (x1+x2)  (x1+x3) (x1+x3) |
| 0 | 0 |
Утверждение 8.
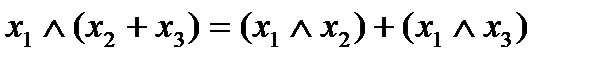 ,
,
конъюнкция дистрибутивна по отношению к сумме по модулю два.
| x1 | x2 | x3 | x2+x3 | x1  (x2+x3) (x2+x3) | x1  x2 x2 | x1  x3 x3 | (x1  x2)+(x1 x2)+(x1  x3) x3) |
| 1 | |||||||
| 0 | 0 |
Определение.Две функции назовем одинаковыми, если они зависят от одного и того же набора переменных и их значения совпадают на каждом из наборов своих переменных.
Определение
Переменная x булевой функции f(x…) называется существенной, если существует набор значений остальных переменных функции, что изменение значения переменной при данном наборе остальных переменных изменяет значение функции.
Пример: x1 и x2 - существенные переменные (x1 по 8 –му и по 5-му наборам; x2
по 6 и 8 наборам).
x3 - не существенная переменная
| x1 | x2 | x3 | f |
| 1 | |||
Определение
Две функции равны, если они одинаковы после отбрасывания несущественных переменных.
