Метод наименьших квадратов
Построение линейной регрессии сводится к оценке ее параметров – 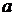 и
и 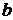 . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Согласно методу наименьших квадратов неизвестные параметры выбираются таким образом, чтобы сумма квадратов отклонений выборочных значений
. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). Согласно методу наименьших квадратов неизвестные параметры выбираются таким образом, чтобы сумма квадратов отклонений выборочных значений 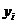 от значений
от значений 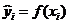 , найденных по уравнению регрессии, была минимальной:
, найденных по уравнению регрессии, была минимальной:
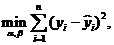
где минимум ищется по неизвестным параметрам 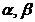 , которые входят в зависимость
, которые входят в зависимость 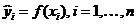 .
.
Найденные значения параметров, которые минимизируют указанную сумму квадратов разностей, называются оценками неизвестных параметров по методу наименьших квадратов. Полученные оценки подставляются в функцию 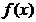 вместо неизвестных коэффициентов. В результате после подстановки получается функциональная зависимость, в которой нет неизвестных параметров, построенную таким образом функцию будем обозначать
вместо неизвестных коэффициентов. В результате после подстановки получается функциональная зависимость, в которой нет неизвестных параметров, построенную таким образом функцию будем обозначать 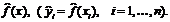 Именно эту зависимость будем рассматривать как усредненную зависимость изучаемого показателя от объясняющего фактора, она и является выборочным (эмпирическим) уравнением регрессии.
Именно эту зависимость будем рассматривать как усредненную зависимость изучаемого показателя от объясняющего фактора, она и является выборочным (эмпирическим) уравнением регрессии.
После нахождения уравнения регрессии вычисляется остаточная сумма квадратов 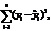 по величине которой можно судить о качестве соответствия эмпирической функции
по величине которой можно судить о качестве соответствия эмпирической функции 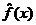 имеющимся в наличии статистическим наблюдениям. Перебирая разные функциональные зависимости и действуя подобным образом можно практически подобрать наиболее удачную функцию для описания имеющихся данных.
имеющимся в наличии статистическим наблюдениям. Перебирая разные функциональные зависимости и действуя подобным образом можно практически подобрать наиболее удачную функцию для описания имеющихся данных.
Т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 1.2):
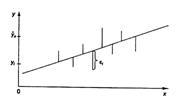
Рис. 1.2. Линия регрессии с минимальной дисперсией остатков.
Как известно из курса математического анализа, чтобы найти минимум функции (1.2), надо вычислить частные производные по каждому из параметров 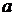 и
и 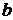 и приравнять их к нулю.
и приравнять их к нулю.
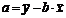 ,
, 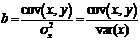 , (1.5)
, (1.5)
где 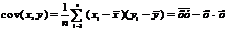 – ковариация признаков
– ковариация признаков 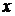 и
и 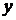 ,
, 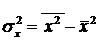 – дисперсия признака
– дисперсия признака 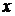 и
и
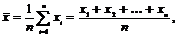
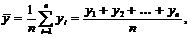
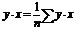 ,
, 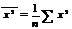
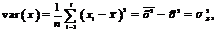
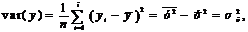
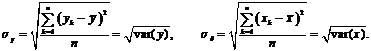
Ковариация – числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий.
Дисперсия – характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
Математическое ожидание – сумма произведений значений случайной величины на соответствующие вероятности.
