Понятие непрерывности функции в точке
3.1. Три определения непрерывной в точке x0
Функции
Определение 1.Функция называется непрерывной в точке x0 , если
1) функция y = f(x) определена в самой точке x0 и в некоторой ее окрестности;
2) 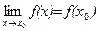 .
.
Заметим, что 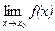 не всегда совпадает со значением функции y = f(x) в точке x0 (даже в тех случаях, когда этот предел существует). Функции, для которых
не всегда совпадает со значением функции y = f(x) в точке x0 (даже в тех случаях, когда этот предел существует). Функции, для которых 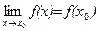 (непрерывные функции), – это наиболее используемые как в самой математике, так и в ее приложениях функции.
(непрерывные функции), – это наиболее используемые как в самой математике, так и в ее приложениях функции.
В основе понятия непрерывности лежит понятие предела функции. Используя определение предела «на языке ε – δ», можно дать «на языке ε – δ» и определение непрерывной функции.
Определение 2. Функция y = f(x) называется непрерывной в точке x0, если она определена в точке x0 и в некоторой
ее окрестности и для 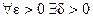 такое, что
такое, что
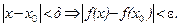
Если ввести обозначения x – x0 = ∆x, f(x) – f(x0) = ∆y,то можно дать еще одно определение непрерывной в точке x0 функции, равносильное двум данным определениям.
Определение 3.Функция y = f(x) непрерывна в точке x0, если бесконечно малому приращению ее аргумента в точке x0 будет соответствовать бесконечно малое приращение функции, то есть если 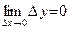 .
.
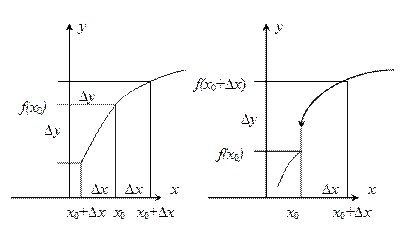
Геометрическая иллюстрация поведения
Функции в случаях
1) 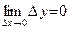 2)
2) 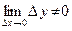
|
3.3. В каком случае функция y = f(x) называется
непрерывной на замкнутом промежутке [a , b]?
Функция должна быть непрерывна в каждой внутренней точке промежутка [a, b], при этом в граничных точках промежутка должна иметь место так называемая односторонняя непрерывность:
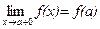 ,
, 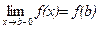 .
.
В каком случае будут непрерывны функции
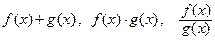 ?
?
Сумма, произведение и частное двух функций будут непрерывными в точке x0 функциями, если каждая из функций f(x) и g(x) будет непрерывна в точке x0, причем в случае функции 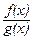 должно быть выполнено условие:
должно быть выполнено условие: 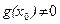 .
.
Это утверждение следует из определения 1 непрерывной в точке функции и теореме о пределе суммы, произведения и частного двух функций.
Что можно сказать о непрерывности простейших
Элементарных функций?
Каждая из простейших элементарных функций непрерывна в каждой точке своей области определения. Непрерывность каждой элементарной функции доказывается отдельно. Мы сделаем это, когда перейдем к решению задач.
Перечислить условия, при которых сложная
функция y = f(g(x)) будет непрерывна в точкеx0
1. Функция y = f(g(x)) должна быть определена в точке x0
и в некоторой ее окрестности.
2. Функция g(x) должна быть непрерывна в точке x0 .
3. Функция y = f(z) должна быть непрерывна в точке z0 , причем z0= g(x0).

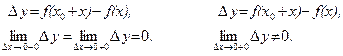 y = f(x) непрерывна в График функции y = f(x) точке x0. терпит в точке x0разрыв.
y = f(x) непрерывна в График функции y = f(x) точке x0. терпит в точке x0разрыв.