В связи с чем возникло понятие предела функции?

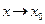Одной из основных задач математического анализа является изучение поведения функции в достаточно малой окрестности некоторой точки x₀ или при . В связи с этим возникло понятие предела функции при и при . В зависимости от поведения функции y = f(x) геометрически возможны следующие ситуации (рис. 2.1–2.4).

Рис. 2.1 Рис. 2.2

Рис. 2.3 Рис. 2.4

2.3. Определение предела функции в случаях 1–4

Определение 1.

.

Определение означает, что число A будет пределом функции y = f(x) при 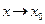в том случае, если для x, попавших в достаточно малую проколотую окрестность точки , соответствующие значения f(x) попадут в сколь угодно малую окрестность числа A (рис. 2.1).

Заметим, что в определении предела не требуется, чтобы функция была определена в самой (∙)x₀. Достаточно, чтобы функция была определена в проколотой окрестности (∙)x₀.

Определение 2.

.

Определение означает, что для достаточно больших x соответствующие значения f(x) будут отличаться от A сколь угодно мало ( рис. 2.2).

Определение 3.

.

Определение означает, что для x, попавших в достаточно малую проколотую окрестность (∙)x₀, соответствующие значения f(x) становятся сколь угодно большими (рис. 2.3).

Определение 4.

.

Определение означает, что для x достаточно больших соответствующие значения f(x) становятся сколь угодно большими (рис. 2.4).

2.4. Определение односторонних пределов функции

В тех случаях, когда возникает необходимость в изучении поведения функции y = f(x) или только в левосторонней (x < x₀) или правосторонней (x > x₀) полуокрестностях точки x₀ , используются так называемые односторонние пределы функции, для которых приняты обозначения обозначение предела слева) и (обозначение предела справа).

;

.

Из определения предела следует

.

Пример 1.Исходя из определения 1, доказать, что

.

Решение.

.

Таким образом, задача сводится к доказательству существования числа δ > 0 для любого наперед заданного ε > 0 ( в частности, сколь угодно малого):

Таким образом, если взять , то

,

а это и означает, что .

Заметим, что величина δ зависит от ε , причем чем меньше ε , тем меньше δ.

Чтобы проиллюстрировать определение геометрически, преобразуем данную функцию, разложив ее числитель на множители:

.

График заданной функции при будет совпадать с графиком линейной функции y = 4x–1(рис. 2.5).

Стрелки на графике функции иллюстрируют тот факт, что функция не определена в точке x₀ = 2.

	Рис.2.5

Пример 2.Изобразить схематично график функции

y= f(x), удовлетворяющей условиям:

Решение. график функции вблизи точки x = -2 прижимается к прямой x = –2 , устремляясь вниз.

график функции y = f(x) вблизи точки x = 2 прижимается к прямой x = 2 , устремляясь вверх.

график функции y = f(x) при x→∞ прижимается к оси Ox.

график функции пересекает ось Ox в точках . Один из возможных вариантов графика такой функции имеет вид:

	Рис. 2.6

Пример 3.Используя символику теории предела, записать особенности поведения функции y = f(x), график которой изображен на рис. 2.7.

	Рис. 2.7

Решение.