Системы линейных алгебраических уравнений

Лабораторное занятие № 2

Тема: Решение систем линейных уравнений

с помощью формул Крамера (2 час.)

Учебно-познавательные цели занятия:

ознакомиться с методикой решения систем линейных уравнений с помощью формул Крамера

Воспитательные цели: Развивать алгоритмическую культуру студентов, повышать интерес к предмету в процессе решения задач

Развивающаяцель – развитие творческих способностей студентов.

На лабораторном занятии формируются понятия:

-решения системы линейных уравнений:

- совместной, несовместной, определенной и неопределенной систем;

На занятии формируются знания:

- формул Крамера;

умения:

- вычислять определители различными способами;

- решать системы линейных уравнений методом Крамера

навыки:

- аргументированного письменного изложения собственной точки зрения;

- критического восприятия информации

компетенции:

- ОК-1–владение культурой мышления, способностью к восприятию, обобщению и анализу информации, постановке цели и выбору путей ее достижения;

- ОК-2–умением логически верно, аргументированно и ясно строить устную и письменную речь;

- ОК-11–способностью представить современную картину мира на основе естественнонаучных, математических знаний, ориентироваться в ценностях бытия, жизни, культуры;

- ПК-1 - способностью использовать основные законы естественнонаучных дисциплин в профессиональной деятельности, применять методы математического анализа и моделирования, теоретического и экспериментального исследования;

- ПК-25 - способностью к обобщению и статистической обработке

Материально-техническое оборудование:

мультимедийный проектор, ноутбук, презентация «Решение систем линейных уравнений методом Крамера».

ПЛАН ЗАНЯТИЯ

1. Инструктаж по ТБ.

2.Проверка знаний студентов — их теоретической готовности к выполнению заданий по каждой из следующих тем:

1. Система трех линейных уравнений с тремя неизвестными;

2. Решение системы трех линейных уравнений с тремя неизвестными методом Крамера;

3. Общее описание задания.

4. Выполнение заданий.

5. Оформление отчета о лабораторной работе.

6. Анализ

ГЛОССАРИЙ

№ п/п	Новые понятия	Содержание
	Обратная матрица для квадратной матрицы А	Обратной матрицей для квадратной матрицы A называется матрица A-1, такая, что верно равенство: A×A-1=A-1×A=E.
	Вырожденная и невырожденная матрицы	Квадратная матрица называется вырожденной, если ее определитель равен нулю, в противном случае матрица называется невырожденной.
	Решение системы линейных уравнений	Решением системы линейных уравнений называется упорядоченный набор n чисел, при подстановке которых вместо переменных в систему, каждое уравнение обращается в верное равенство.
	Формулы Крамера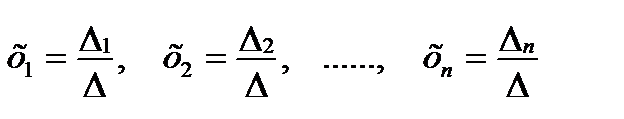
	Элементарные преобразования	К элементарным преобразованиям относят: перестановку 2-х уравнений; умножение уравнения на число, отличное от нуля; прибавление к одному уравнению другого уравнения, умноженного на какое-либо число; вычеркивание уравнения вида .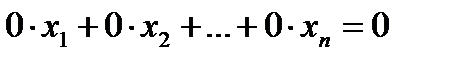
	Теорема Кронекера-Капелли	Система линейных уравнений имеет решение тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы.

ХОД ЗАНЯТИЯ

1. Инструктаж по ТБ в компьютерном классе.

2. На лабораторном занятии используется работа в парах (или малых группах).

Студентам необходимо:

- ознакомиться с основными теоретическими сведениями по каждой

из рассматриваемых тем;

- ответить на контрольные вопросы по по каждой

из рассматриваемых тем;

- изучить решение общих исходных практических заданий;

- выполнить представленные задания;

- оформить отчет о лабораторной работе;

- защитить лабораторную работу

Необходимый для повторения теоретический материал по теме:

"Решение систем линейных уравнений по формулам Крамера"

Системы линейных алгебраических уравнений

Общий видсистемы линейных алгебраических уравнений следующий:

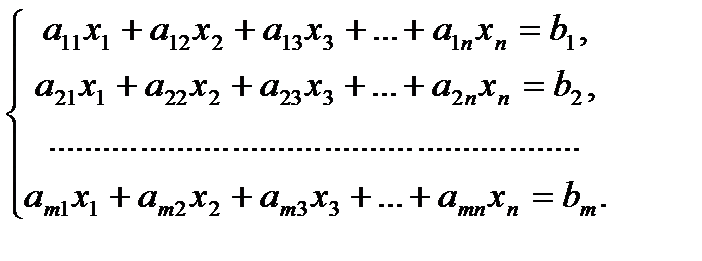(2),

где а_ij, i=1,...m; j=1,…n—неизвестные величины, называемые коэффициентами системы уравнений. Первый индекс означает номер уравнения, второй—номер неизвестного, при котором стоит коэффициент; b_i, i=1,…m—известные величины, называемые свободными членами, или правыми частями уравнений; x_j, j=1,…n—неизвестные переменные величины (или просто неизвестные).

Система (2)—система линейных уравнений, т.к. все неизвестные входят во все уравнения только в первой степени.

Матрица А, составленная из коэффициентов системы, называется матрицей системы.

Матрица системы, дополненная столбцом свободных членов А│В, называется расширенной матрицей системы:

А= 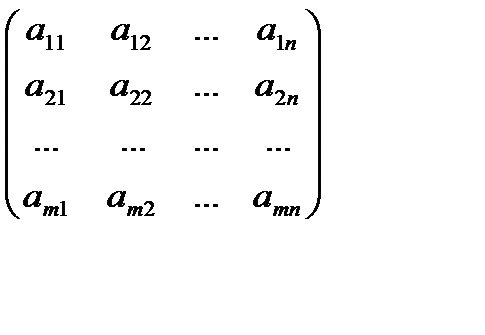, А│В=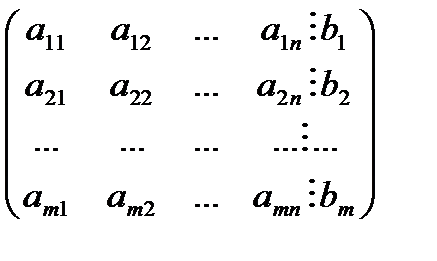

Систему (2) можно записать в матричном виде АХ=В,

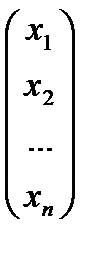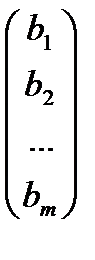где Х= ; В= (3).

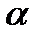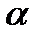Набор чисел ₁, ₂,…, 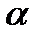_n — решение системы, если при подстановке x₁= 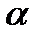₁; x₂= 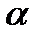₂;…, x_n= 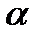_n все уравнения системы превращаются в верные тождества.

Решить систему значит найти все её решения или доказать, что не существует ни одного её решения. Если решений бесконечное множество, то указать способ нахождения каждого из них.

Система линейных уравнений называется совместной, если она имеет хотя бы одно решение.

Система, не имеющая ни одного решения, называется несовместной.

Если совместная система имеет единственное решение, то она называется определённой, а если более одного решения, то неопределенной.

Две системы алгебраических линейных уравнений называют эквивалентными или равносильными, если они имеют одно и то же множество решений.