По какой формуле вычисляются наибольшие касательные напряжения в исследуемой точке тела и на каких площадках они возникают?
Найдем угол наклона площадки 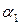 , при котором касательное
, при котором касательное
напряжение 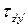 , определяемое по формуле (6.3), принимает экстремальное значение. Для этого возьмем производную
, определяемое по формуле (6.3), принимает экстремальное значение. Для этого возьмем производную 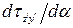 и приравняем ее к нулю:
и приравняем ее к нулю:
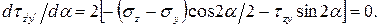
Отсюда
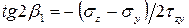 . (6.8)
. (6.8)
 Сопоставляя равенства (6.8) и (6.5), мы видим, что
Сопоставляя равенства (6.8) и (6.5), мы видим, что
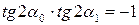 ,
,
следовательно, 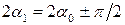 или
или 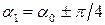 .
.
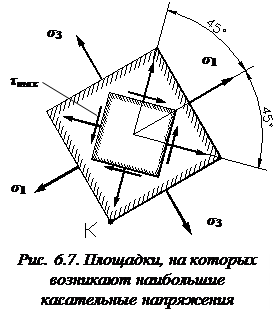
Таким образом, для данной точки существуют две взаимно перпендикулярные площадки, на которых возникают равные по закону парности экстремальные касательные напряжения 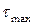 . Эти площадки расположены под углом
. Эти площадки расположены под углом 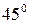 к главным площадкам
к главным площадкам
(рис. 6.7), на которых «действуют» главные напряжения  и
и 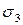 .
.
Абсолютное значение экстремальных касательных напряжений определяется по формуле
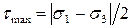 .
.
В общем случае нагружения на площадках, на которых возникают наибольшие касательные напряжения, возникают и нормальные напряжения. Последние равны половине суммы главных напряжений 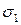 и
и 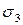 .
.
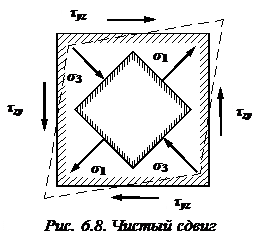
Если же, например, на площадках, где возникают наибольшие касательные напряжения, нормальные напряжения отсутствуют, то эти площадки называются площадками чистого сдвига.
Вернемся к чистому сдвигу. Чему в этом случае равны главные напряжения и в каких направлениях они возникают?
Напомним, что при чистом сдвиге в поперечных сечениях стержня возникают только касательные напряжения 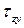 .
.
 По закону парности касательных напряжений
По закону парности касательных напряжений 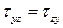 .Напряженное состояниев рассматриваемой точке являетсяплоским. Пусть
.Напряженное состояниев рассматриваемой точке являетсяплоским. Пусть 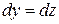 (рис. 6.8).
(рис. 6.8).
По формуле (6.4) найдем, что 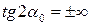 .
.
Тогда
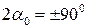 и
и 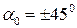 .
.
По формуле (6.6) получим:
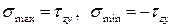 .
.
Следовательно, главные напряжения при чистом сдвиге равны:
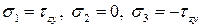 .
.
Их направления показаны на рис. 6.8.
Наибольшие касательные напряжения равны:
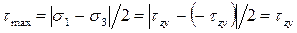 .
.
Таким образом, чистый сдвиг можно рассматривать как простую комбинацию растяжения и сжатия под углом 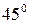 .
.
ПРЯМОЙ ИЗГИБ
Стержень с прямолинейной осью, работающий на изгиб, называют балкой. Балки являются одним из важнейших элементов всех строительных конструкций, а также многих конструкций, применяемых в машиностроении, кораблестроении и в других отраслях техники.
Первым вопрос о прочности балок поставил в 1638 г. Галилей в своей книге «Беседы и математические доказательства, касающиеся двух новых отраслей науки». В 1826 г., то есть спустя почти два столетия, французский ученый Клод Луи Мари Анри Навье (Navier, 1785 – 1836 гг.) практически завершил создание теории изгиба балок. Этой теорией мы, по существу, пользуемся и по настоящее время.
7.1. Какая деформация называется изгибом?
Изгибом называется такой вид деформации, при котором первоначально прямолинейная ось стержня искривляется.
7.2. Какие перемещения возникают при изгибе балки?
В результате изгиба произвольная точка, лежащая на оси балки, перемещается в направлении вертикальной оси y и продольной оси z. Вертикальное перемещение обычно обозначают буквой v и называют его прогибом балки. Продольное перемещение точки обозначают буквой u.
Касательная, проведенная к точке, расположенной на изогнутой оси балки, будет повернута по отношению к прямолинейной оси на некоторый угол. Этот угол, как показывают многочисленные опытные данные, оказывается равным углу поворота 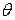 поперечного сечения балки, проходящего через рассматриваемую точку.
поперечного сечения балки, проходящего через рассматриваемую точку.
Таким образом, три величины v, u и 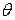 являются компонентами перемещения произвольного поперечного сечения балки при изгибе.
являются компонентами перемещения произвольного поперечного сечения балки при изгибе.
В дальнейшем мы покажем, что 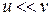 , поэтому при расчете балки на изгиб продольным перемещением u пренебрегают.
, поэтому при расчете балки на изгиб продольным перемещением u пренебрегают.
7.3. Какой изгиб называется прямым?
Если балка изгибается в плоскости действия внешней нагрузки, то такой изгиб называется прямым.
Прямой изгиб стержня будет иметь место в том случае, если силовая плоскость совпадает с одной из главных плоскостей. Силовой плоскостью называется плоскость, в которой действуют внешние нагрузки, а главной плоскостью – плоскость, которая проходит через продольную ось стержня z и одну из главных центральных осей инерции поперечного сечения (например, через ось x или ось y).
