Найдем критерии надежности системы методом дифференциальных уравнений

На основании вероятностного графа, представленного на рис. 15, запишем систему дифференциальных уравнений.

Начальные условия: P₀(0)=1, P₁(0)=0, P₂(0)=0.

Применим преобразование Лапласа к левой и правой частям уравнений полученной системы:

Преобразуем систему:

Представим систему в матричном виде:

Отсюда

Выполним обратное преобразование Лапласа и подставим заданное значение t=8760:

Р20(8760)= 0,000011387473744519446063

Вероятность безотказной работы: P(t)=1 – P₂(t)

Р(8760)=

Среднее время безотказной работы определим по формуле

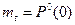, где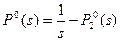

Подставляя выражение для P₂⁰(s), получим:

Подставив значение s=0, получим:

mt= 7,693*10⁸ ч

Для определения коэффициента готовности составим по графу состояний систему дифференциальных уравнений с учетом обратного перехода из состояния 2:

При t→∞ система примет следующий вид:

После преобразований система примет вид:

Коэффициент готовности:

K_Г =1 – P₂

Подставляя значение P₂, получим:

K_Г=1–

Найдем коэффициент готовности данной системы методом Половко

Запишем вероятности системы по графу, представленному на рис.15:

Коэффициент готовности системы:

,

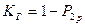
Коэффициент готовности системы, рассчитанный методом Половко, совпал с коэффициентом готовности системы, рассчитанным методом дифференциальных уравнений.

K_Г= 0,99998375140154236533

Среднее время восстановления:

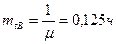
Вероятность успешного использования системы:

R(t)=K_ГP(t)

R(8760) ≈ 0,999972363950342268765

Восстанавливаемая система без резервирования

Расчетно-логическая схема:

Рис. 16. Восстанавливаемая система без резервирования

Рассчитаем характеристики надежности данной системы с помощью формул для восстанавливаемой системы с частично нагруженным резервом, считая λ₀ = ∞.

Получим:

Формула для вероятности успешного использования:

R(t)=K_ГP(t)

Подставив значения исходных данных, получим:

m_t=12500 ч

m_tв= 0,125 ч

K_Г ≈ 0,9999900001

R(t)=0,4961832326

Исследование влияния различных параметров на надежность систем

Влияние интенсивности потока отказов

Для невосстанавливаемой резервированной системы с дробной кратностью с нагруженным резервом

На рисунках (Рис. 17 и 18) приведены сравнительные графики для отображения влияния интенсивности потока отказов на вероятность безотказной работы системы и на среднее время безотказной работы.

Рис. 17 «Влияние интенсивности потока отказов на вероятность безотказной работы невосстанавливаемой резервированной системы с дробной кратностью»

Рис. 18 «Влияние интенсивности потока отказов на среднее время безотказной работы невосстанавливаемой резервированной системы с дробной кратностью»