Вводные понятия и определения. элементы

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ

ОДНОЙ ПЕРЕМЕННОЙ.

Учебное пособие для студентов

заочной формы обучения

МАГНИТОГОРСК

ВВОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ. ЭЛЕМЕНТЫ

ТЕОРИИ ЛОГИКИ.

Приступая к изучению математического анализа, студент уже имеет представление о понятии множеств, среди которых выделяют такие, как числовые поля. Напомним обозначения числовых множеств: - множество натуральных чисел; - множество целых чисел (кольцо целых чисел); - мно -жество рациональных чисел (поле рациональных чисел); - множество действительных чисел (основное числовое поле);

- множество комплексных чисел. Между всеми этими множествами существуют соответствующие соотношения:

Важную роль в математическом анализе играет понятие ме- ры близости элементов различных множеств (понятие нормы или, связанного с ней, понятия метрики). Для числовых мно -жеств этой мерой является абсолютная величина или модуль.

ОПРЕДЕЛЕНИЕ . Абсолютной величиной (модулем) числа называется само число , если , и число , если .

Абсолютная величина числа обладает следующими свой- ствами, которые часто используются в различных областях математики

1). 2).

3). 4).

ЗАМЕЧАНИЕ. Для комплексного числа модуль равен , и для него все свойства сохраняются.

Действительные числа изображаются точками числовой прямой. На некоторой прямой (будем считать её располо -женной горизонтально) выберем положительное направление, начало отсчёта О и единицу масштаба .

О 1 М

Для изображения положительного числа возьмём на нашей прямой справа от точки О мочку М на расстоянии ( в принятом масштабе), равном данному числу ; для изобра -жения отрицательного числа возьмём точку слева от на -чала отсчёта О на расстоянии, равном ; числу бу -дет отвечать точка O - начало отсчёта. Таким образом мы устанавливаем взаимно однозначное соответствие между все- ми точками прямой и множеством действительных чисел: каж -дое действительное число будет изображено одной опреде -лённой точкой прямой, а каждая точка прямой является изо -бражением одного определённого действительного числа. В дальнейшем мы будем обозначать одним и тем же символом 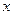и действительное число 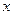и точку 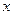числовой оси.

Множество всех действительных чисел 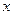, удовлетворяю-щих неравенству , где , называется отрезком (сегментом) и обозначается . Интервалом назы -вается множество всех действительных чисел 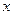, удовлетво –ряющих неравенству . Аналогично определяются понятия полуинтервалов и

Мы будем рассматривать также бесконечные интервалы, введя несобственные точки (числа) и , т.е.

Пусть . 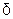- окрестностью точки называется интер- вал . Проколотой 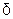- окрестностью точки называется .

ОПРЕДЕЛЕНИЕ. Множество действительных чисел называется ограниченным сверху (снизу), если существует число такое, что для всякого числа выпол- няется неравенство .

Множество называется ограниченным, если для всякого выполняется неравенство (т.е. ). Число 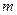называется нижней гранью множества , а 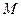- верхней гранью.

Исходя из свойств действительных чисел, можно утверж -дать, что среди всех нижних граней найдётся наибольшая, а среди всех верхних граней - наименьшая.. Их обозначают или - точная нижняя грань ( infiinum - наинизший ); или - точная верхняя грань множества (supremum - наивысший).

В дальнейшем для сокращения записи и для построения определений мы будем пользоваться некоторыми логическими символами и отношениями.

Квантор существования - - соответствует словам «сущес- твует», «найдётся». Квантор общности - - соответствует словам «для всякого», «для любого», «для каждого», «для всех».

Будем называть высказыванием всякое повествовательное предложение, в отношении которого имеет смысл утверждать, истинно оно или ложно. Высказывания условимся обозначать .

Импликация (если , то ) или ( влечёт ) означает высказывание, которое ложно в том или только в том случае, когда истинно, а - ложно.

Эквивалентность - ( тогда и только тогда, когда ) означает логическую равносильность высказываний и .

Конъюнкция означает : высказывание « и » считается истинным тогда и только тогда, когда оба высказывания и истинны.

Дизъюнкция означает высказывание или считается истинным высказыванием тогда и только тогда, когда истинно хотя бы одно из данных высказываний.

Отрицание - означает «не » - истинно, если ложно и, наоборот, ложно, если истинно.

Отрицание некоторого свойства, содержащего кванторы и , получается заменой каждого квантора на двойственный и заменой «свойства» на его отрицание. При этом, если , то .

Необходимое и достаточное условия: всякое высказывание , из которого следует , называется достаточным условием для . Высказывание в этом случае называется необхо -димым для высказывания .

Если высказывания и таковы, что из каждого из них вытекает другое, т.е. и , то говорят, что каждое из высказываний и является необходимым и доста -точным для другого и пишут .

§ 2. ПОСЛЕДОВАТЕЛЬНОСТЬ, ПРЕДЕЛ ПОСЛЕДО –

ВАТЕЛЬНОСТИ.

2.1 Числовые последовательности и операции с ними.

ОПРЕДЕЛЕНИЕ 1. Если каждому числу натурального ряда чисел: 1, 2, …., , … , по определённому закону, ста - вится в соответствие некоторое действительное число , то множество занумерованных действительных чисел

(1)

называется числовой последовательностью или просто последовательностью.

Число называется общим членом последовательности, - порядковым номером последовательности. Зная порядко- вый номер и общий член последовательности, можем указать любой член последовательности. Сокращённо последователь -ность (1) обозначается символом . Например символом

обозначается последовательность: и таким же образом, по общему члену последовательности можно определить любой член последовательности.

Введём понятие арифметических операций над числовыми последовательностями. Пусть даны произвольные последова-тельности и . Суммой этих последовательностей называется последовательность , разностью - после- довательность , произведением - последовательность и частным - последовательность . ( При определении операции необходимо требовать , чтобы все элементы последовательности были отличны от нуля.

ОРПЕДЕЛЕНИЕ 2. Последовательность называется ограниченной сверху (снизу) если существует такое действи- тельное число 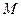(число 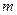), что каждый элемент после -довательности удовлетворяет неравенству

. (1)

При этом число 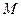(число 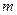) называется верхней (нижней ) гранью последовательности , а условия (1) называются условиями ограниченности последовательности сверху (снизу).

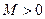ОПРЕДЕЛЕНИЕ 3. Последовательность называется ограниченной, если она ограничена сверху и снизу, т.е. если существует число , такое что для всех .

Например, последовательность ограничена снизу, но неограниченна сверху;

последовательность ограничена сверху числом 1, а снизу числом 0, т.е. просто ограничена;

последовательность не ограничена ни сверху, ни снизу.

2.2. Бесконечно большие и бесконечно малые последовательности.

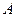О п р е д е л е н и е 1. Последовательность называется бесконечно большой, если для любого положительного числа существует номер , начиная с которого (т.е. для всех ) выполняется неравенство . (2)

Например, последовательность являет-ся бесконечно большой, а неограниченная последовательность не является бесконечно большой, так как для сколь угодно больших номеров существуют элементы равные 1 и невозможно выполнение неравенства (2).

О п р е д е л е н и е «. Последовательность называется бесконечно малой, если для любого положительного числа существует номер , начиная с которого все элементы последовательности удовлетворяют неравенству .

Например, последовательность является бесконечно малой. В самом деле, для произвольного 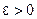существует номер , начиная с которого (для всех ) выполняется неравенство: .

Основные свойства бесконечно малых последователь- ностей.

1 Сумма или разность бесконечно малых последова- тельностей является бесконечно малой последова -тельностью. (более того, как следствие, алгебраическая сумма (т.е. сумма или разность) любого конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью).

2 Бесконечно малая последовательность - ограничена.

3 Произведение ограниченной последовательности на бесконечно малую - бесконечно малая последователь- ность. ( в частности, при умножении бесконечно малой последовательности на любое число получим бесконеч- но малую последовательность).

4 Произведение двух бесконечно малых последователь- ностей - бесконечно малая последовательность (как следствие, произведение любого конечного числа бес- конечно малых последовательностей является бесконеч- но малой последовательностью).

5 Если все элементы бесконечно малой последователь –ности равны одному и тому же числу 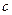, то

Следующая теорема устанавливает связь между бесконечно малыми и бесконечно большими последовательностями.

ТЕОРЕМА 1 Если - бесконечно большая последова- тельность то является бесконечно малой, и наоборот, если - бесконечно малая последовательность, то последовательность является бесконечно большой.

Д о к а з а т е л ь с т в о. Следует отметить, что у бесконечно большой последовательности только конечное число элементов может быть равно нулю Это следует из определения бесконечно большой последовательности, так как существует номер , начиная с которого для всех элементов выполняется неравенство . Это означает, что для всех элементы последовательности не равны нулю и поэтому последовательность имеет смысл, если её элементы начинать рассматривать начиная с номера . Докажем, что последовательность бесконечно малая. Возьмём произвольное число 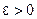. Для числа можем указать номер , начиная с которого ве элементы последовательности удовлетворяют неравенству . Тогда, начиная с этого номера, будет выполняться неравенство . Таким образом доказано, что последовательность является бесконечно малой. Аналогично доказывается второе утверждение теоремы.

2.3. Предел числовой последовательности. Свойства сходящихся последовательностей.

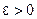О п р е д е л е н и е 1 Число называется пределом число- вой последовательности при , если для любого числа существует номер , начиная с которого все элементы последовательности удовлетворяют неравенству

. (3)

Символически это записывается так , или при .

Если последовательность имеет предел, то её называют сходящейся; ели же предела не существует, то её называют расходящейся.

Замечание 1 В соответствии с этим определением, всякая бесконечно малая последовательность имеет предел и этот предел равен нулю.

Замечание 2 Бесконечно большие последовательности иногда называют последовательностями, сходящимися к бесконечности и записывают .

Замечание 3. Если , то последовательность является бесконечно малой. Следовательно, любой элемент сходящейся последовательность можно представить в виде

, (4)

где - элемент бесконечно малой последовательности.

Замечание 4. Неравенство (3) равносильно неравенствам или . Последнее неравен -ство означает, что элементы находятся в - окрестности точки . В соответствии с этим получаем ещё одно опреде -ление сходящейся последовательности:

О п р е д е л е н и е 2. Последовательность называется сходящейся, если существует число такое, что в любой - окрестности этого числа находятся все элементы последова -тельности , начиная с некоторого номера.

Рассмотрим примеры сходящихся последовательностей.

1. Последовательность сходится и предел этой последовательности равен 1. В самом деле, разность и для доказательства сходимости достаточно убедиться, что последовательность является бесконечно малой. Для произ -вольного можем взять любой номер . Тогда . Следовательно, для всех чисел , удовлетворяющих неравенству , будет выполнено , т.е. последова- тельность в самом деле бесконечно малая.
2. Последовательность сходится и имеет пределом число . В самом деле

. Из этих неравенств получается . Так как при , , то для произвольно взятого , выбрав номер из условия , получим при .

Основные свойства сходящихся последовательностей:

1. Сходящаяся последовательность имеет только один предел.
2. Сходящаяся последовательность ограничена.
3. Алгебраическая сумма сходящихся последовательностей является сходящейся последовательностью, причём, если , то .
4. Произведение сходящихся последовательностей является сходящейся последовательностью, причём, если , то .

5. Частное двух сходящихся последовательностей и

, при условии, что предел не равен нулю,

является сходящейся последовательностью, предел

которой равен частному пределов последовательностей

и

6. Из сходимости последовательности следует

сходимость последовательностей

для любых чисел и .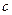

7. Если все элементы некоторой сходящейся последовательности , начиная с некоторого номера, удовлетворяют неравенству , то и предел этой последовательности - удовлетворяет такому же неравенству, т.е. .

8. Если элементы сходящихся последовательностей

и , начиная с некоторого номера, удовлетво-

ряют неравенству , то их пределы удовлетворя-

ют тому же неравенству, т.е. .

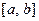9. Если все элементы сходящейся последовательности находятся в отрезке , то её предел также находится в этом отрезке.

10. Пусть и - сходящиеся последовательности, причём . Пусть, кроме этого, начи- ная с некоторого номера, элементы последовательнос- ти удовлетворяют неравенству: . Тогда последовательность также сходится и имеет предел, равный .

Замечание В соответствии с теоремой 1 из 1.3, любая

последовательность вида , является бесконечно малой, т.е. . Поэтому, учитывая свойства 3 – 7 сходящихся последовательностей, можем легко вычислять следующие пределы:

Пример 1. Найти предел . Разделим чис- тель и знаменатель дроби на . В результате получим

В дальнейшем, при вычислении пределов такого вида, ни к чему повторять такую последовательность операций. Легко проверить и следует запомнить следующее правило:

ПРАВИЛО: Если в дроби старшая степень числителя меньше старшей степени знаменателя, то предел равен нулю; если старшая степень числителя больше старшей степени знаменателя, то предел равен бесконечности; если старшие степени числителя и знаменателя совпадают, то предел равен отношению коэффициентов перед старшими степенями.

Рассмотрим ещё один пример:

Пример 2. Вычислить предел

.

Под знаком предела находится неопределённое выражение вида . Для вычисления такого предела желательно сначала получить дробь и затем использовать правило. Для этого умножим и разделим это выражение на сумму корней, чтобы получить в числителе разность квадратов. Получим:

2.4. Монотонные последовательности.

О п р е д е л е н и е Последовательность называется убы- вающей, если для всех выполняется неравенство ; последовательность называется невозраста -ющей, если для всех выполняется неравенство ; последовательность называется возрастаю -щей, если для всех выполняется неравенство ; последовательность называется неубываю -щей, если для всех выполняется неравенство . Во всех этих случаях последовательность называется монотонной.

Например, 1. Последовательность является невозрастающей. Она ограничена сверху своим первым элементом 1, а снизу числом 0.

2. Последовательность является неубывающей. Она ограничена снизу числом 1, а сверху неограниченна.

3. Последовательность является возрастающей и ограниченной с двух сторон - снизу числом 0, сверху - числом 1.

Признак сходимости монотонной последовательности Если неубывающая (невозрастающая) последовательность ограничена сверху (снизу), то она сходится, или, иначе, этот признак можно сформулировать так: если монотонная последовательность ограничена с обоих сторон, то она сходится.

Замечание: условие ограниченности монотонной последова -тельности является необходимым и достаточным условием сходимости.

Следствием этого признака является так называемая

ТЕОРЕМА (О вложенных отрезках) Пусть дана бесконечная система отрезков и пусть длины этих отрезков: стремятся к нулю при . Тогда существует, и притом единственная, точка 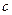, принадлежащая всем отрезкам этой системы.

Доказательство. Прежде всего следует заметить, что точка 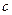, общая для всех отрезков, может быть только одна. В самом деле, если бы нашлась ещё одна точка , принадлежащая всем отрезкам, то и весь отрезок принадлежал бы всем отрезкам . Тогда для всех выполнялось бы неравенство . Но это невозможно, так как при . Докажем теперь существование точки 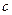. Так как последовательность отрезков является стягивающейся, то последовательность левых концов является неубывающей, а последова –тельность правых концов - невозрастающей. Поскольку обе эти последовательности ограничены (все элементы этих

последовательностей содержатся в отрезке ), то по признаку сходимости они обе сходятся. Но из того, что последовательность является бесконечно малой, следует, что обе последовательности имеют тот же предел, который мы можем обозначить 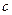, причём для всех выполняется неравенство , т.е. точка 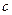- общая для всех отрезков.

Ещё одним следствием признака сходимости монотонных последовательностей является доказательство существования предела последовательности , которая ограничена снизу числом 2, а сверху - числом 3. Предел этой последовательности считаем, по определению равным , т.е.

.