Пример использования критерия Михайлова

Для анализа статической устойчивости.

Критерий Михайлова является частотным критерием устойчивости. В его основу положен принцип аргумента [1], известный из теории функций комплексного переменного.

Рассмотрим использование частотного критерия Михайлова для анализа устойчивости простейшей электрической системы , рассмотренной в разд. 3.2, 3.3.

Исходя из вида характеристического уравнения (3.13), запишем характеристический многочлен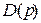

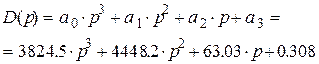(3.14)

Осуществляя подстановку 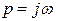в (3.14) получим характеристический вектор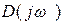

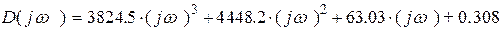(3.15)

Разделим действительную и мнимую составляющие вектора ,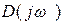

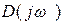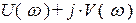= (3.16)

где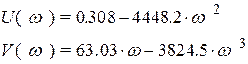

Вектор 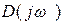, изображенный в декартовых координатах на плоскости, при изменении - ¥ < 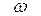< ¥ вращается и концом вектора описывается кривая, которая называется годографом характеристического уравнения.

Практическая формулировка критерия Михайлова: система будет устойчива, если при возрастании w от 0 до ¥ годограф, начинаясь на положительной части вещественной оси, проходит последовательно в положительном направлении 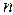квадрантов, где 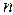– степень характеристического уравнения.

Такое перемещение годографа соответствует повороту вектора 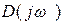на угол 0,5 p .

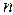Для построения годографа определим точки пересечения

с вещественной 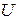и мнимой 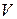осями:

а) пересечение годографа с осью 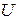происходит при 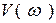=0

=

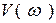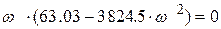
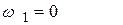
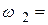
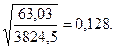
Таким образом , первая точка пересечения при 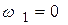соответствует 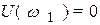; вторая точка при 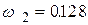соответствует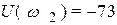

б)пересечение годографа с осью 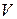происходит при

= ;

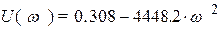
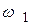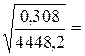
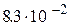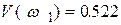
Выбираются только положительные значения корней, так как 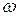изменяется от 0 до ¥ .

Для построения графика зададимся рядом значений 0<w<¥ и рассчитываем соответствующие значения 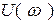и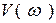

Таблица 3.1

w		5·10-2	8·10-2	10-1	2·10-1	¼	¥
U	0.308 000,308	-10.8	-28.16	-44.17	-177.6	¼	-¥
V		2.67	3.08	2.47	-17.99	¼	-¥

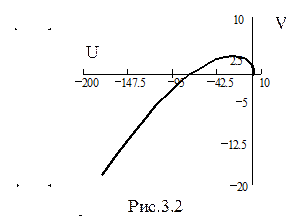Годограф характеристического уравнения (3.13) представлен на рис. 3.2

На основании полученного годографа, используя критерий Михайлова, можно сделать вывод об устойчивости системы.

Реализация задачи анализа устойчивости в Mathcad PLUS 6.0

Лабораторная работа N 3

Тема: Анализ статической устойчивости ЭС.

Анализ по корням характеристического уравнения.

Определение эквивалентного сопротивления системы относительно 6 узла

Мощность и напряжение балансирующего узла:

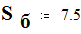
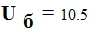
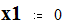
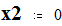
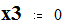
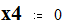
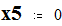
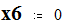
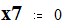
Given

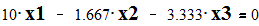
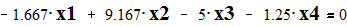
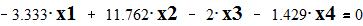
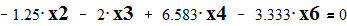
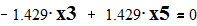
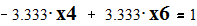
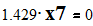
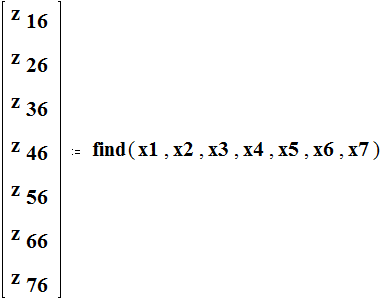
Эквивалентное сопротивление системы относительно 6 узла

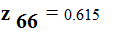
Перевод в относительные единицы: 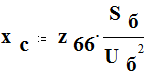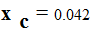o.е.

Параметры генератора и системы :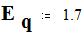

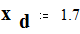
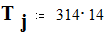
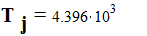
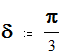
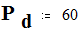
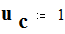
переходное сопротивление :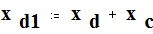

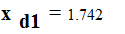
Коэффициент характеристического уравнения :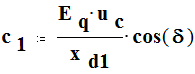

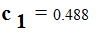
Определение корней характеристического уравнения

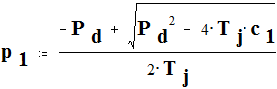
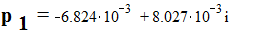
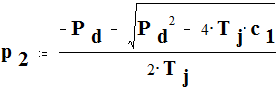
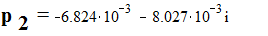
Вывод: Система статически устойчива по теореме Ляпунова