Контрольная работа № 3. Задание № 3.1. Вычислить приближенно по формуле трапеций (1–5) и по формуле Симпсона
Задание № 3.1. Вычислить приближенно по формуле трапеций (1–5) и по формуле Симпсона (6–10) следующие интегралы:
1. 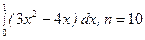 ; 6.
; 6. 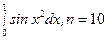 ;
;
2. 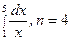 ; 7.
; 7. 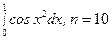 ;
;
3. 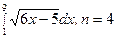 ; 8.
; 8. 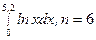 ;
;
4. 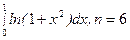 ; 9.
; 9. 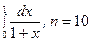 ;
;
5. 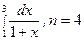 ; 10.
; 10. 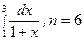 .
.
Задание № 3.2. Разложить в степенной ряд решение дифференциального уравнения и найти первые три члена разложения.
1. 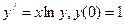 .
.
2. 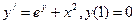 .
.
3. 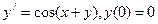 .
.
4. 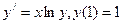 .
.
5. 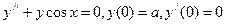 .
.
6. 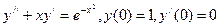 .
.
7. 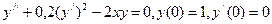 .
.
8. 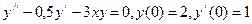 .
.
9. 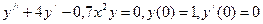 .
.
10. 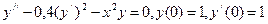 .
.
Задание № 3.3. Найти область сходимости степенного ряда.
1. 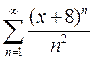 ; 6.
; 6. 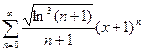 ;
;
2. 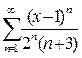 ; 7.
; 7. 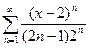 ;
;
3. 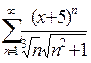 ; 8.
; 8. 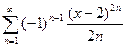 ;
;
4. 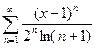 ; 9.
; 9. 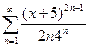 ;
;
5. 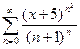 ; 10.
; 10. 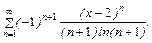
Задание № 3.4. Вычислить указанный определенный интеграл с точностью до 0,001, используя разложение подынтегральной функции в степенной ряд.
1. 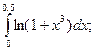 6.
6. 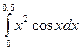 ;
;
2. 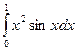 ; 7.
; 7. 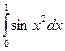 ;
;
3. 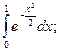 8.
8. 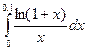 ;
;
4. 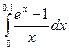 ; 9.
; 9. 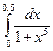 ;
;
5. 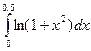 ; 10.
; 10. 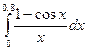 .
.
Задание № 3.5.Решить систему дифференциальных уравнений с помощью характеристического уравнения.
1. 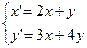 6.
6. 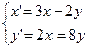
2. 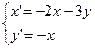 7.
7. 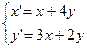
3. 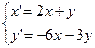 8.
8. 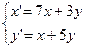
4. 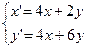 9.
9. 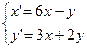
5. 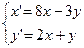 10.
10. 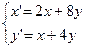
Задание № 3.6. Найти разложение в степенной ряд по степеням x решения дифференциального уравнения, записать первые три, отличных от нуля, члена разложения.
1. y' = e3x + 2xy2, y(0) = 1;
2. y' = x + ey, y(0) = 0;
3. y' = х2 + 2у2, у(0) = 0,2;
4. y' = х2 + ху + у2, у(0) = 0,5;
5. y' = 2cosx – xy2, у(0) = 1;
6. y' = х + х2 + у2, у(0) = 1;
7. y' = х2у2 + у 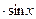 , у(0) = 1/2 ;
, у(0) = 1/2 ;
8. y' = ху – у2, у(0) = 0,2;
9. y' = х 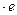 х + 2у2, у(0) = 0;
х + 2у2, у(0) = 0;
10. y' = ху + ех, у(0) = 0.
Задание № 3.7. Решить задачу путем составления дифференциального уравнения.
1. Записать уравнение кривой, проходящей через точку А (2, 4) и обладающей следующим свойством: длина отрезка, отсекаемого на оси абсцисс касательной, проведенной в любой точке кривой, равна кубу абсциссы точки касания.
2. Записать уравнение кривой, проходящей через точку А (1, 5) и обладающей свойством: длина отрезка, отсекаемого на оси ординат любой касательной, равна утроенной абсциссе точки касания.
3. Записать уравнения кривых, для которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, равную 2/3 абсциссы точки касания.
4. Записать уравнения кривых, для которых расстояние от любой касательной до начала координат равно абсциссе точки касания.
5. Записать уравнения кривых, для которых точка пересечения любой касательной с осью абсцисс имеет абсциссу, вдвое меньшую абсциссы точки касания.
6. Записать уравнение кривой, проходящей через точку А (0, –2), если известно, что угловой коэффициент касательной в любой ее точке равен утроенной ординате этой точки.
7. Записать уравнения кривых, для которых отрезок касательной к кривой, заключенный между осями координат, делится в точке касания пополам.
8. Записать уравнение кривой, проходящей через точку А (1, 2), если известно, что произведение углового коэффициента касательной в любой ее точке и суммы координат точки касания равно удвоенной ординате этой точки.
9. Записать уравнения кривых, для которых длина отрезка, отсекаемого касательной на оси ОY, равна квадрату абсциссы точки касания.
10. Записать уравнение кривой, каждая касательная к которой пересекает прямую у = 1 в точке с абсциссой, равной удвоенной абсциссе точки касания.
Приложение 4
