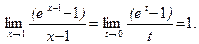Введение новой переменной
Во многих случаях, чтобы найти 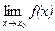 , имеет смысл сделать замену
, имеет смысл сделать замену 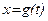 , при этом если
, при этом если 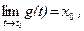 то
то 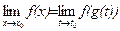 .
.
Пример 1.Найти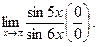
Решение.Введем новую переменную 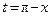 или
или 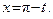 Очевидно, при
Очевидно, при 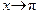 переменная
переменная 
Тогда
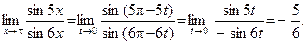
Использованы формулы приведения и первый замечательный предел.
Пример 2.Найти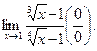
Решение.Введем новую переменную 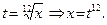
При 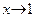 переменная
переменная 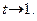
Тогда 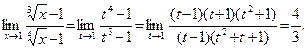
3. Раскрытие неопределенностей вида 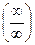
При нахождении 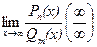 , где Pn(x) и Qm(x) – многочлены, используется метод деления числителя и знаменателя на xk , где k – наибольшее из чисел m и n. Аналогичный прием используется и при нахождении пределов иррациональных неопределенностей вида
, где Pn(x) и Qm(x) – многочлены, используется метод деления числителя и знаменателя на xk , где k – наибольшее из чисел m и n. Аналогичный прием используется и при нахождении пределов иррациональных неопределенностей вида 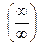 .
.
Пример 1. 
Решение.Разделим числитель и знаменатель дроби на x3. Тогда
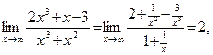
так как 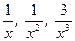 – бесконечно малые величины при
– бесконечно малые величины при 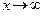 .
.
Пример 2. 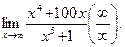
Решение.Разделим числитель и знаменатель дроби на x5. Тогда
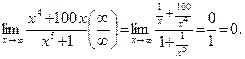
Пример 3. 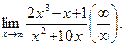
Решение.Разделим числитель и знаменатель дроби на x3. Тогда
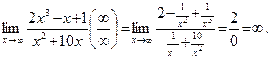
Сравнивая полученные в примерах 1–3 результаты, можно сделать вывод:
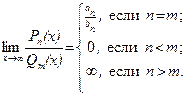
(an и bn – коэффициенты при xn многочленов Pn(x) и Qn(x) соответственно).
Этот вывод позволяет в простейших случаях находить 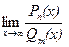 без каких-либо преобразований.
без каких-либо преобразований.
Например, 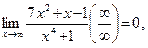
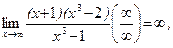
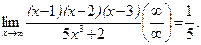
Перейдем к решению более сложных примеров.
Пример 4. 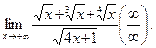
Решение.Разделим числитель и знаменатель дроби на 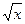 :
:
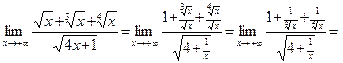
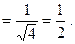
Заметим, что в этом примере наивысшие степени переменной в числителе и знаменателе равны (и там, и там это 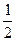 ), поэтому ответ оказался равным отношению коэффициентов при
), поэтому ответ оказался равным отношению коэффициентов при 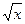 .
.
Пример 5. 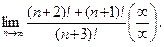
Решение.Напомним, что 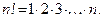 Разделим почленно числитель на знаменатель:
Разделим почленно числитель на знаменатель:
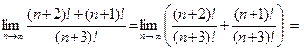
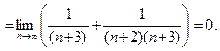
4. Раскрытие неопределенностей вида 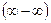
и 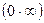
Каждую из неопределенностей 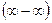 и
и 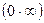 стараются свести к неопределенностям
стараются свести к неопределенностям 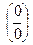 и
и 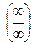 . Далее используют соответствующий способ раскрытия неопределенного выражения полученного вида.
. Далее используют соответствующий способ раскрытия неопределенного выражения полученного вида.
Пример 1.Найти 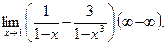
Решение.Вынесемзнак минуса из знаменателей за общую скобку и приведем разность к общему знаменателю 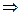
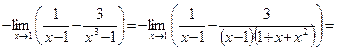
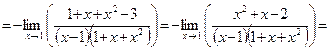

Пример 2.Найти 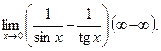
Решение. 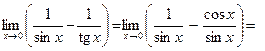
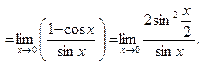
Осталось воспользоваться первым замечательным пределом
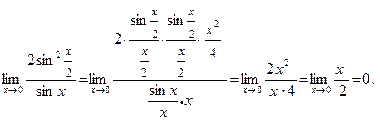
Пример 3.Найти 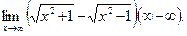
Решение.Умножим и поделим заданное выражение на сумму 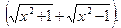 Тогда
Тогда
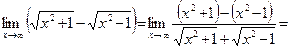
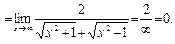
Пример 4.Найти 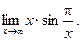
Решение. 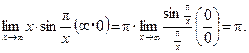
Использован первый замечательный предел:
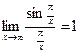 (
( 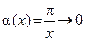 при
при 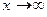 ).
).
Пример 5.Найти 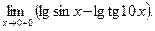
Решение.Воспользуемся тем, что
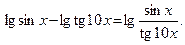
Тогда
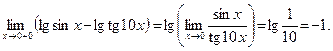
Использованы непрерывность логарифмической функции и первый замечательный предел.
5. Раскрытие неопределенностей вида 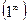
Неопределенности вида 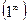 раскрываются с помощью второго замечательного предела, который можно записывать двумя способами:
раскрываются с помощью второго замечательного предела, который можно записывать двумя способами:
(3) 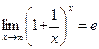 или
или 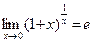 . (4)
. (4)
Напомним, что второй замечательный предел получен на основании равенства
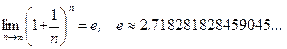 ,
,
полученного в теории последовательностей.
Особенность пределов (3) и (4) состоит в том, что в основании степени и в (3), и в (4) к числу 1 прибавляется бесконечно малая величина, а в показателе степени стоит бесконечно большая величина, в точности обратная той, которая прибавляется к 1. В результате имеет место неопределенное выражение 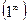 . Это наблюдение позволяет записать (3) и (4) в виде
. Это наблюдение позволяет записать (3) и (4) в виде 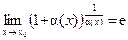 , где α(x) → 0 при x → x0 . (5)
, где α(x) → 0 при x → x0 . (5)
Запись (5) позволяет формально достаточно просто использовать второй замечательный предел при раскрытии неопределенностей вида 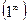 .
.
Перейдем к вычислению пределов.
Пример 1. 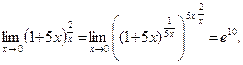
так как 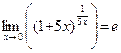 .
.
Пример 2. 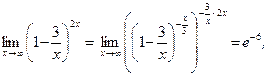
так как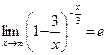 .
.
Использованный при решении примеров прием очень прост: показатель степени умножают и делят на одно и то же выражение, играющее в примере роль α(x). В первом примере 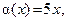 во втором
во втором 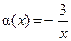 .
.
Пример 3. 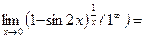
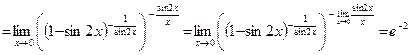 .
.
Использованы непрерывность степенно-показательной функции и второй и первый замечательные пределы.
Пример 4. 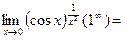
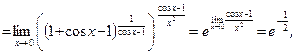
так как
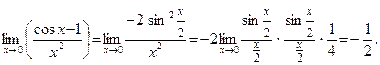
Пример 5. 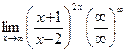 .
.
Найдем 
Это означает, что имеет место неопределенность (1∞), и мы имеем право использовать второй замечательный предел: 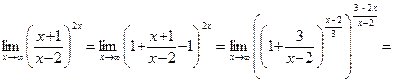
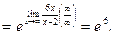
Пример 6.  .
.
В этом примере, в отличие от всех предыдущих,  Это означает, что второй замечательный предел применять нельзя, тем более, что заданное выражение никакой неопределенности при x → ∞ не представляет:
Это означает, что второй замечательный предел применять нельзя, тем более, что заданное выражение никакой неопределенности при x → ∞ не представляет:
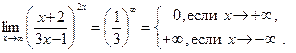
Примеры 7–10 решены с помощью следствий второго замечательного предела:
1. 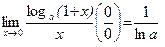 . 2.
. 2. 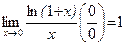 .
.
3. 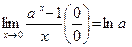 . 4.
. 4. 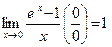 .
.
Заметим, что следствие 2 является частным случаем следствия 1, а следствие 4 – частным случаем следствия 3.
Все следствия легко доказываются. Докажем, например, следствие 1:
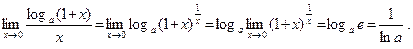 Использованы непрерывность логарифмической функции и второй замечательный предел.
Использованы непрерывность логарифмической функции и второй замечательный предел.
Следствия 1–4 позволяют раскрывать неопределенные выражения вида 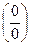 , содержащие логарифмическую и показательную функции.
, содержащие логарифмическую и показательную функции.
Пример 7. 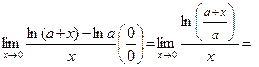
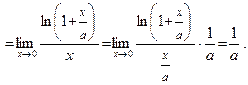
Использовали следствие 2.
Пример 8. 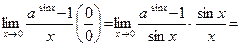
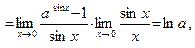
так как
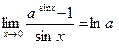 (следствие 3), а
(следствие 3), а 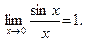
Пример 9. 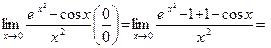
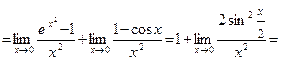
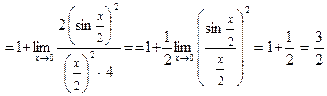 .
.
Пример 10. 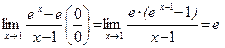 ,
,
здесь 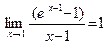 по следствию 4, роль бесконечно малого аргумента играет разность (x – 1) при x → 1. Можно было сделать замену x – 1 = t .
по следствию 4, роль бесконечно малого аргумента играет разность (x – 1) при x → 1. Можно было сделать замену x – 1 = t .
Тогда