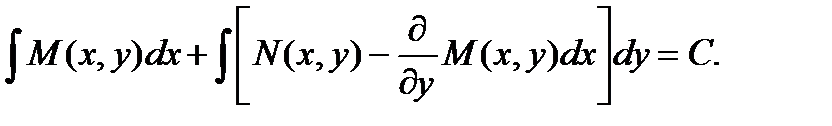Однородные уравненияУравнения, приводящиеся к однородным
Определение. ДУ первого порядканазывается соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида: 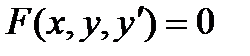 Определение. ДУ
Определение. ДУ 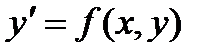 называется уравнением с разделяющимися переменными, если его можно записать в виде
называется уравнением с разделяющимися переменными, если его можно записать в виде 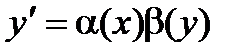 . Такое У-е можно представить в виде:
. Такое У-е можно представить в виде:
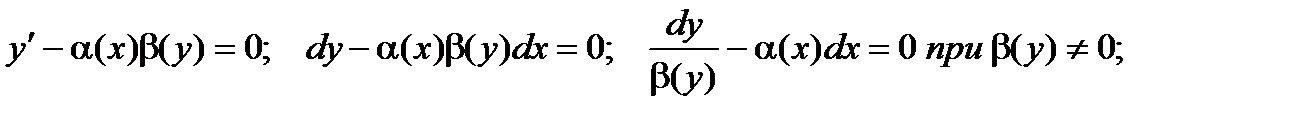 Перейдем к новым обознач
Перейдем к новым обознач 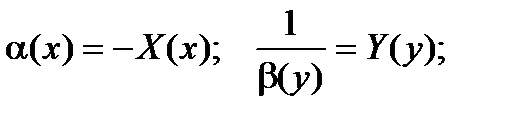 Получаем:
Получаем: 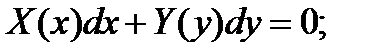
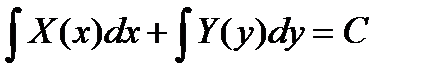 После нахождения соответствующих интегралов получается общее решение ду с разделяющимися переменными. Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение. Определение. ДУ вида
После нахождения соответствующих интегралов получается общее решение ду с разделяющимися переменными. Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение. Определение. ДУ вида 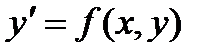 называется однородным, если его правая часть f(x, y) есть однородная ф-я нулевого измерения относительно своих аргументов. Любое уравнение вида
называется однородным, если его правая часть f(x, y) есть однородная ф-я нулевого измерения относительно своих аргументов. Любое уравнение вида 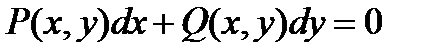 является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения. Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с раздел перем. Рассмотрим однородное уравнение
является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения. Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с раздел перем. Рассмотрим однородное уравнение 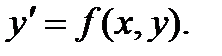 Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать:
Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать: 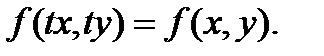 Т.к. параметр t произвольный, то
Т.к. параметр t произвольный, то 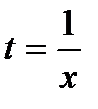 . Получаем:
. Получаем: 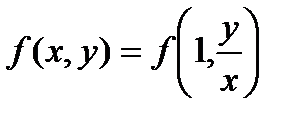 Правая часть полученного равенства зависит фактически только от одного аргумента
Правая часть полученного равенства зависит фактически только от одного аргумента 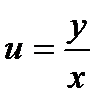 , т.е.
, т.е. 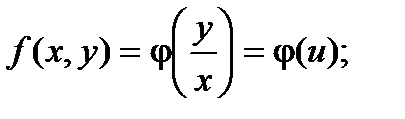 Исходное ду можно записать в виде:
Исходное ду можно записать в виде: 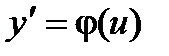 Далее заменяем y = ux,
Далее заменяем y = ux, 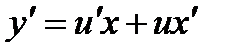 .
. 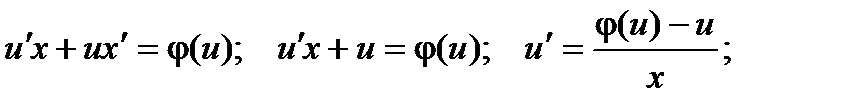 таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.
таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u. 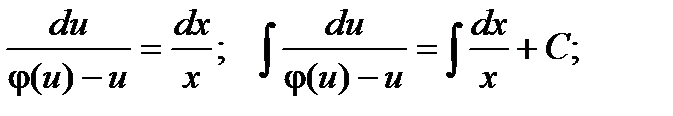 Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.
Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.
С разд перем. Кроме уравнений, описанных выше, существует класс уравнений, которые с помощью определенных подстановок могут приведены к однородным. Это уравнения вида 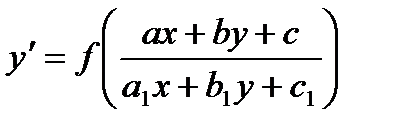 . Если определитель
. Если определитель 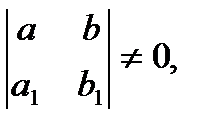 то переменные могут быть разделены подстановкой
то переменные могут быть разделены подстановкой 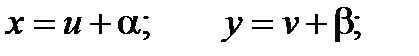 где a и b - решения системы уравнений
где a и b - решения системы уравнений 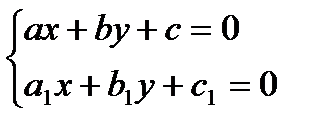
30. Уравнения в полных дифференциалах
Опр ДУ первого порядка вида: 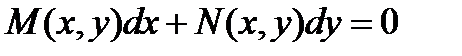 называется уравнением в полных дифф, если левая часть этого уравнения представляет собой полный диф некоторой ф-ии
называется уравнением в полных дифф, если левая часть этого уравнения представляет собой полный диф некоторой ф-ии 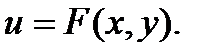 Интегр такого у-я сводится к нахождению функции u, после чего решение легко находится в виде:
Интегр такого у-я сводится к нахождению функции u, после чего решение легко находится в виде: 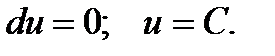 То, для решения надо определить: 1) в каком случае левая часть Ур-я представляет собой полный дифф функции u; 2) как найти эту функцию. Если дифф форма
То, для решения надо определить: 1) в каком случае левая часть Ур-я представляет собой полный дифф функции u; 2) как найти эту функцию. Если дифф форма 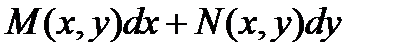 является полным дифференциалом некоторой функции u, то можно записать:
является полным дифференциалом некоторой функции u, то можно записать: 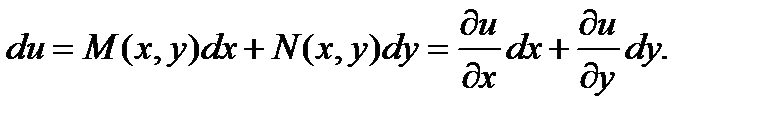 Т.
Т. 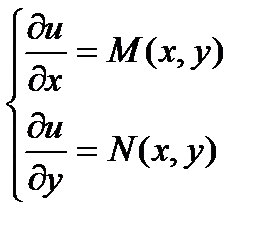 . Найдем смешанные производные второго порядка, продиф первое Ур-е по у, а второе – по х:
. Найдем смешанные производные второго порядка, продиф первое Ур-е по у, а второе – по х: 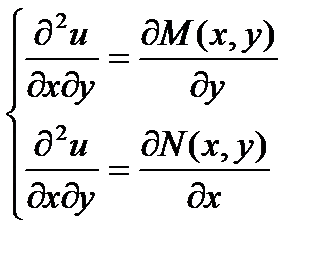 Приравнивая левые части Ур-й, получаем необходимое и достаточное условие того, что левая часть ду является полным дифф. Это условие – условие тотальности.
Приравнивая левые части Ур-й, получаем необходимое и достаточное условие того, что левая часть ду является полным дифф. Это условие – условие тотальности. 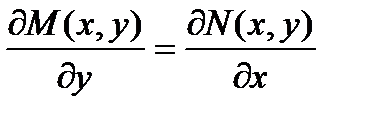 найдем функцию u Проинтегрируем равенство
найдем функцию u Проинтегрируем равенство 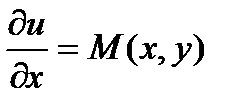 :
: 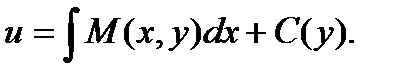 Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию С(у), т.к. при интегрировании переменная у полагается постоянным параметром. Определим функцию С(у). Продифференцируем полученное равенство по у.
Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию С(у), т.к. при интегрировании переменная у полагается постоянным параметром. Определим функцию С(у). Продифференцируем полученное равенство по у. 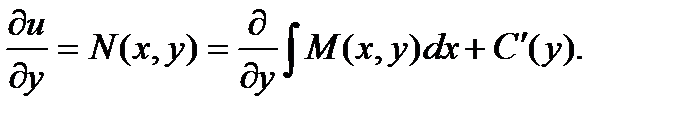 Откуда получаем:
Откуда получаем: 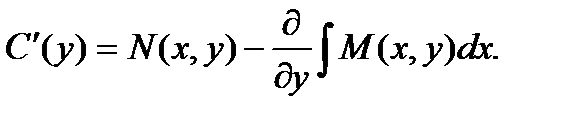 Для нахождения функции С(у) необходимо проинтегрировать приведенное выше равенство. Однако, перед интегрированием надо доказать, что функция С(у) не зависит от х. Это условие будет выполнено, если производная этой функции по х равна нулю.
Для нахождения функции С(у) необходимо проинтегрировать приведенное выше равенство. Однако, перед интегрированием надо доказать, что функция С(у) не зависит от х. Это условие будет выполнено, если производная этой функции по х равна нулю.
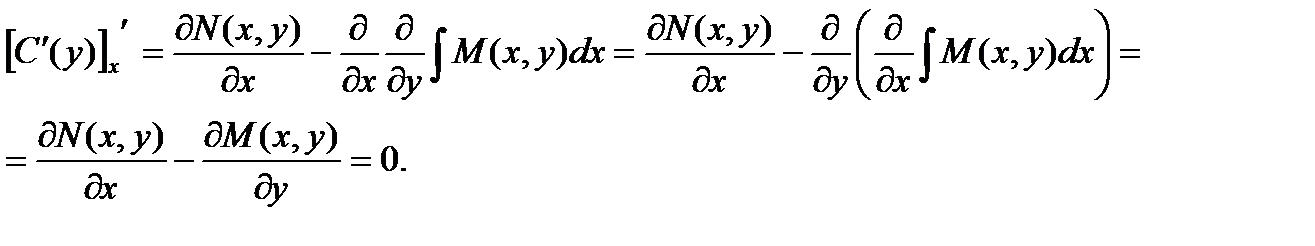 определяем функцию С(у):
определяем функцию С(у): 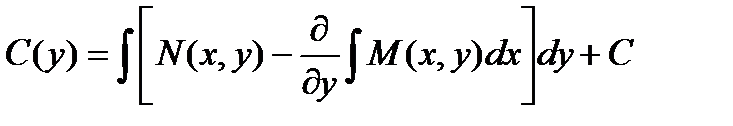 Подставляя этот результат в выр-е для функции u, получаем:
Подставляя этот результат в выр-е для функции u, получаем: 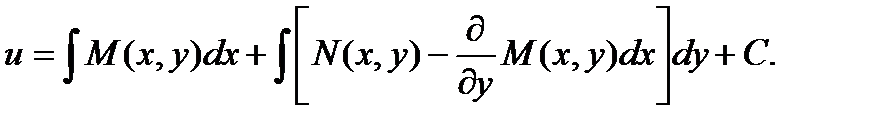 Тогда общий интеграл исходного ду будет иметь вид:
Тогда общий интеграл исходного ду будет иметь вид: