Изменение шага в многошаговых методах

ЦЕЛЬ ЛЕКЦИИ: Показать, как можно на основе так называемого вектора Нордсика, не прибегая к задаче интерполяции, эффективно изменять шаг интегрирования в процессе численного решения обыкновенных дифференциальных уравнений.

Сущность проблемы изменения шага в многошаговых методах сводится к следующему.

В текущий момент времени 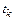в памяти компьютера хранятся вычисленные значения решения 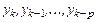и умноженные на 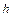значения его производной 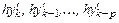в моменты времени 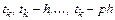. Обозначим их вектором

.

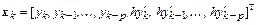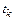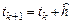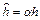Если в момент времени принимается решение об изменении шага интегрирования, т. е. , где , то для выполнения шага интегрирования многошаговым методом необходимы предшествующие значения решения и значения его производной в моменты времени 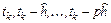. Эти значения образуют вектор

,

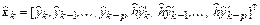причем только 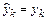. Остальные компоненты вектора 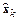должны быть перевычислены. Использование для этой цели интерполяционной процедуры может потребовать значительных вычислительных усилий.

Имеется другой путь. Введем так называемый вектор Нордсика, который для значений временного шага 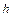и 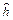имеет вид

,

.

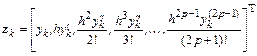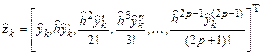Заметим, что 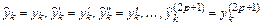, так как эти величины относятся к одному и тому же моменту времени .

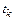Следовательно, значения векторов 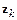и 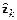связаны простым соотношением

,

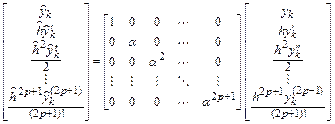или в компактной форме

,

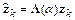где 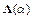– диагональная матрица.

С другой стороны, вектор Нордсика может быть определен посредством следующего линейного преобразования переменных:

,

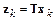где 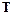– невырожденная матрица преобразования переменных линейного многошагового метода.

Объединение введенных матричных преобразований приводит к линейной системе

,

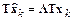из которой для заданного вектора 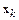можно найти искомый вектор 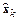. Так как матрица 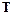имеет невысокий порядок, то такая процедура перехода от 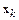к 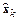оказывается достаточно эффективной.

Рассмотрим, как строится матрица преобразования переменных многошагового метода на примере явного метода Адамса третьего порядка. В этом случае

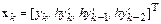
и

.

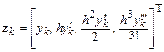При построении матрицы 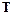воспользуемся тем свойством, что явный

метод Адамса третьего порядка позволяет найти точное решение, описываемое полиномом третьей степени

.

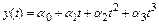Очевидно, что

.

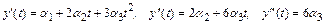Полагая величину 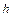постоянной на трех шагах, выберем 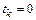, , 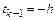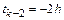и вычислим из соотношений для 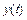, 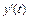зна-чения :

.

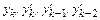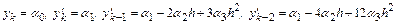Решим эту систему относительно коэффициентов :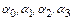

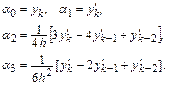
Подставляя значения коэффициентов 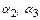в соотношения для 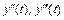, нетрудно найти, что

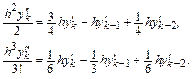
В итоге связь вектора Нордсика явного метода Адамса третьего порядка с вектором 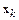имеет следующий вид:

.

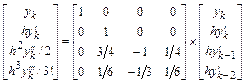Это преобразование переменных имеет место также для неявного метода Адамса четвертого порядка. Действительно, неявный метод Адамса четвертого порядка является трехшаговым методом и для него векторы 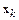и 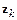такие же, как и для явного метода Адамса третьего порядка.

Наконец, в случае метода Гира третьего порядка (он является трехшаговым) векторы 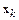и 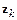соответственно равны

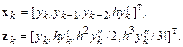
Действуя по аналогии, нетрудно получить, что

.

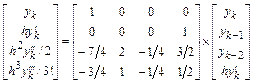В заключение подчеркнем, что для любого многошагового метода можно построить матрицу преобразования переменных. В свою очередь, привлечение матриц 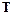и 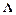позволяет эффективно перевычислять вектор 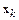при изменении шага интегрирования.

Сделаем ряд практических замечаний по проблеме выбора шага.

Замечание 1. При оценке погрешности интегрирования многошагового метода порядка 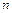по формуле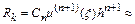 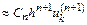необходимо вычислить значение 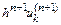. Это легко сделать, используя 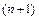-ю компоненту вектора Нордсика на двух соседних шагах:

.

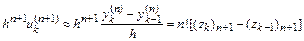Погрешность расчета находится следующим образом:

.

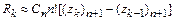Замечание 2. При изменении шага интегрирования 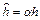локальная погрешность оценивается по формуле

.

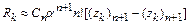Из этого соотношения легко найти параметр :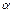

,

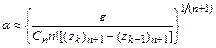где 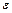– допустимая величина локальной погрешности.