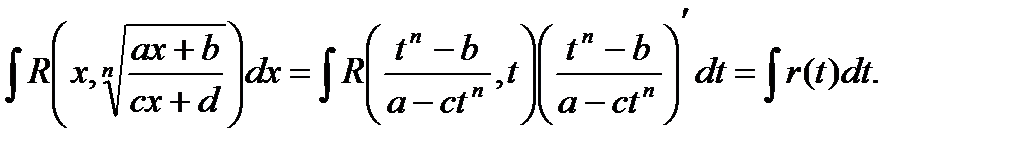Способ. Метод неопределенных коэффициентов
Способ. Тригонометрическая подстановка.
Теорема: Интеграл вида 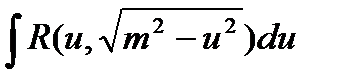 подстановкой
подстановкой 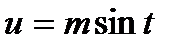 или
или
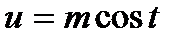 сводится к интегралу от рациональной функции относительно sint или cost.
сводится к интегралу от рациональной функции относительно sint или cost.
Теорема: Интеграл вида 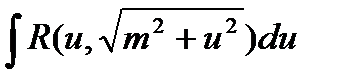 подстановкой
подстановкой 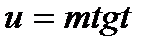 или
или 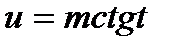 сводится к интегралу от рациональной функции относительно sint и cost.
сводится к интегралу от рациональной функции относительно sint и cost.
Теорема: Интеграл вида 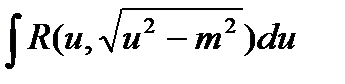 подстановкой
подстановкой 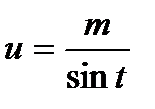 или
или 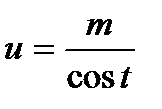 сводится к интегралу от рациональной функции относительно sint или cost.
сводится к интегралу от рациональной функции относительно sint или cost.
2 способ. ПодстановкиЕсли а>0, то интеграл вида 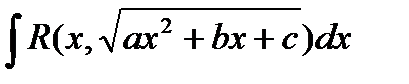 рационализируется подстановкой
рационализируется подстановкой
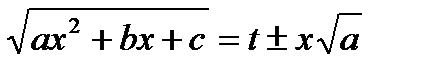 .
.
Если a<0 и c>0, то интеграл вида 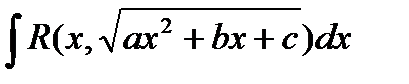 рационализируется подстановкой
рационализируется подстановкой 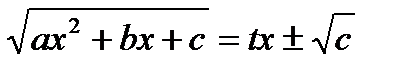 .
.
Если a<0 , а подкоренное выражение раскладывается на действительные множители a(x – x1)(x – x2), то интеграл вида 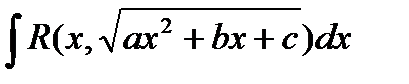 рационализируется подстановкой
рационализируется подстановкой 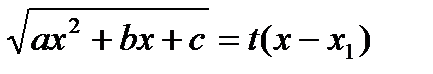 .
.
способ. Метод неопределенных коэффициентов.
Рассмотрим интегралы следующих трех типов:
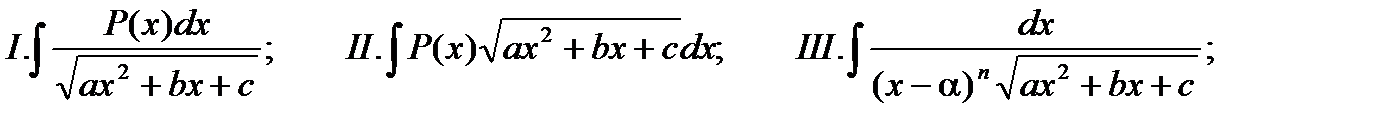
где P(x) – многочлен, n – натуральное число.
Причем интегралы II и III типов могут быть легко приведены к виду интеграла I типа.
Далее делается следующее преобразование:
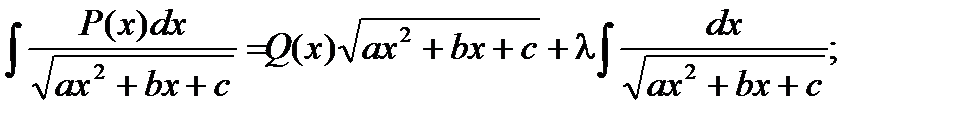
в этом выражении Q(x)- некоторый многочлен, степень которого ниже степени многочлена P(x), а l - некоторая постоянная величина.
Для нахождения неопределенных коэффициентов многочлена Q(x), степень которого ниже степени многочлена P(x), дифференцируют обе части полученного выражения, затем умножают на 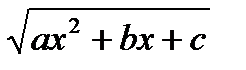 и, сравнивая коэффициенты при одинаковых степенях х, определяют l и коэффициенты многочлена Q(x).
и, сравнивая коэффициенты при одинаковых степенях х, определяют l и коэффициенты многочлена Q(x).
2…. Определение. Нахождение решения уравнения 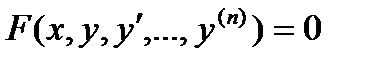 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 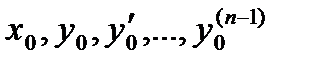 , называется решением задачи Коши.
, называется решением задачи Коши.
Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).
Если функция (n-1) –й переменных вида 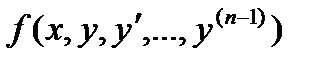 в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по
в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по 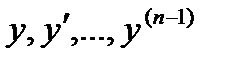 , то какова бы не была точка (
, то какова бы не была точка ( 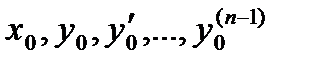 ) в этой области, существует единственное решение
) в этой области, существует единственное решение 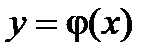 уравнения
уравнения 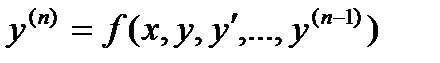 , определенного в некотором интервале, содержащем точку х0, удовлетворяющее начальным условиям
, определенного в некотором интервале, содержащем точку х0, удовлетворяющее начальным условиям 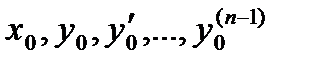 .
.
Дифференциальные уравнения высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов.
Рассмотрим подробнее методы нахождения решений этих уравнений.
№10.1. Непосредственное интегрирование.
Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.
Рассмотрим применение этого метода на примере:
Требуется найти значение интеграла 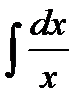 . На основе известной формулы дифференцирования
. На основе известной формулы дифференцирования 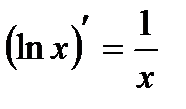 можно сделать вывод, что искомый интеграл равен
можно сделать вывод, что искомый интеграл равен 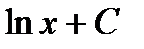 , где С – некоторое постоянное число. Однако, с другой стороны
, где С – некоторое постоянное число. Однако, с другой стороны 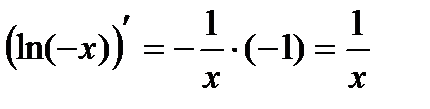 . Таким образом, окончательно можно сделать вывод:
. Таким образом, окончательно можно сделать вывод:
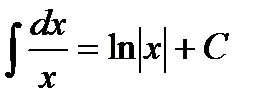
Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.
Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.
2….. Уравнения вида y = f(y’) иx = f(y’).
Решение уравнений, не содержащих в одном случае аргумента х, а в другом – функции у, ищем в параметрической форме, принимая за параметр производную неизвестной функции.
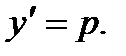
Для уравнения первого типа получаем: 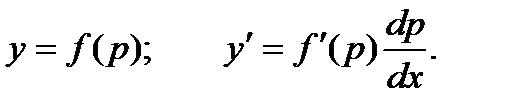
Делая замену, получаем: 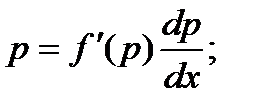
В результате этих преобразований имеем дифференциальное уравнение с разделяющимися переменными.
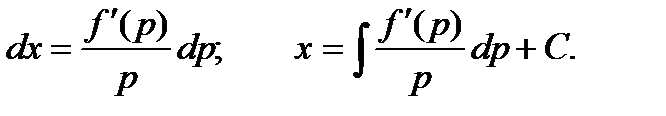
Общий интеграл в параметрической форме представляется системой уравнений:
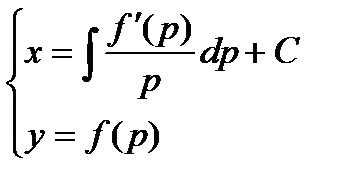
Исключив из этой системы параметр р, получим общий интеграл и не в параметрической форме.
Для дифференциального уравнения вида x = f(y’) с помощью той же самой подстановки и аналогичных рассуждений получаем результат:
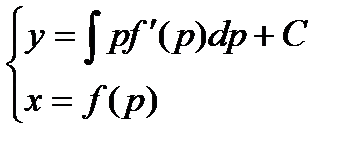
№11.1…. Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.
Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.
Интеграл вида 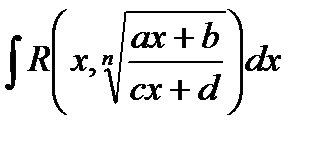 где n- натуральное число.
где n- натуральное число.
С помощью подстановки 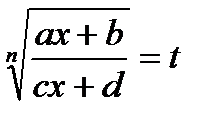 функция рационализируется.
функция рационализируется.
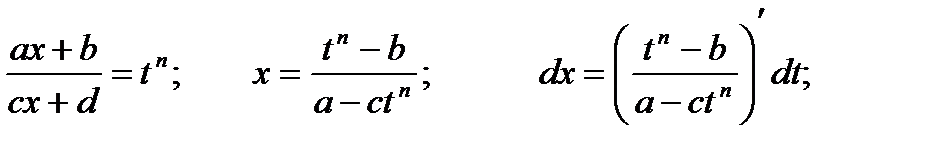
Тогда